题目内容
已知椭圆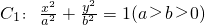 的右焦点为F,上顶点为A,P为C1上任一点,MN是圆C2:x2+(y-3)2=1的一条直径,若与AF平行且在y轴上的截距为
的右焦点为F,上顶点为A,P为C1上任一点,MN是圆C2:x2+(y-3)2=1的一条直径,若与AF平行且在y轴上的截距为 的直线l恰好与圆C2相切.
的直线l恰好与圆C2相切.
(Ⅰ)已知椭圆C1的离心率;
(Ⅱ)若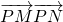 的最大值为49,求椭圆C1的方程.
的最大值为49,求椭圆C1的方程.
解:(Ⅰ)由题意可知直线l的方程为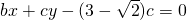 ,
,
因为直线与圆c2:x2+(y-3)2=1相切,所以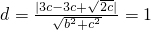 ,即a2=2c2,
,即a2=2c2,
从而 ;(6分)
;(6分)
(Ⅱ)设P(x,y)、圆C2的圆心记为C2,则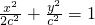 (c>0),又
(c>0),又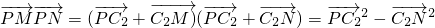 =x2+(3-y)2-1=-(y+3)2+2c2+17(-c≤y≤c).(8分)
=x2+(3-y)2-1=-(y+3)2+2c2+17(-c≤y≤c).(8分)
j当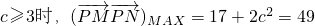 ,解得c=4,此时椭圆方程为
,解得c=4,此时椭圆方程为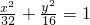 ;
;
k当0<c<3时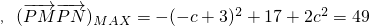 ,
,
解得c=5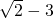 但
但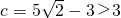 ,故舍去.
,故舍去.
综上所述,椭圆的方程为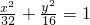 .(14分)
.(14分)
分析:(Ⅰ先得出直线l的方程,再由直线与圆相切得a2=2c2,从而求得离心率;
(II)设P(x,y)由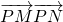 的最大值为49,求得c的值,从而求得椭圆方程.
的最大值为49,求得c的值,从而求得椭圆方程.
点评:本题主要考查直线、圆、椭圆的基本性质及位置关系的应用,渗透向量、函数最值等问题,培养学生综合运用知识的能力.
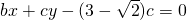 ,
,因为直线与圆c2:x2+(y-3)2=1相切,所以
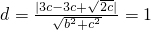 ,即a2=2c2,
,即a2=2c2,从而
 ;(6分)
;(6分)(Ⅱ)设P(x,y)、圆C2的圆心记为C2,则
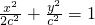 (c>0),又
(c>0),又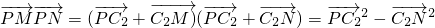 =x2+(3-y)2-1=-(y+3)2+2c2+17(-c≤y≤c).(8分)
=x2+(3-y)2-1=-(y+3)2+2c2+17(-c≤y≤c).(8分)j当
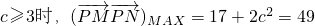 ,解得c=4,此时椭圆方程为
,解得c=4,此时椭圆方程为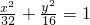 ;
;k当0<c<3时
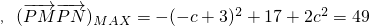 ,
,解得c=5
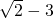 但
但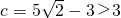 ,故舍去.
,故舍去.综上所述,椭圆的方程为
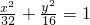 .(14分)
.(14分)分析:(Ⅰ先得出直线l的方程,再由直线与圆相切得a2=2c2,从而求得离心率;
(II)设P(x,y)由
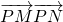 的最大值为49,求得c的值,从而求得椭圆方程.
的最大值为49,求得c的值,从而求得椭圆方程.点评:本题主要考查直线、圆、椭圆的基本性质及位置关系的应用,渗透向量、函数最值等问题,培养学生综合运用知识的能力.

练习册系列答案
相关题目

 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.  ,试用
,试用 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切. 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C