题目内容
(2006•上海)正四棱锥底面边长为4,侧棱长为3,则其体积为
.
| 16 |
| 3 |
| 16 |
| 3 |
分析:由正四棱锥的底面边长求出底面中心到一个顶点的距离,结合侧棱长求出正四棱锥的高,然后直接利用体积公式求体积.
解答:解:如图,正四棱锥P-ABCD中,AB=4,PA=3,
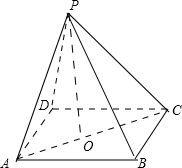
设正四棱锥的高为PO,连结AO,
则AO=
AC=2
.
在直角三角形POA中,PO=
=
=1.
所以VP-ABCD=
•SABCD•PO=
×16×1=
.
故答案为
.

设正四棱锥的高为PO,连结AO,
则AO=
| 1 |
| 2 |
| 2 |
在直角三角形POA中,PO=
| PA2-AO2 |
32-(2
|
所以VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 16 |
| 3 |
故答案为
| 16 |
| 3 |
点评:本题考查了棱锥的体积,解答的关键是熟悉正四棱锥中几个直角三角形,考查了棱锥体积公式的记忆,是基础题.

练习册系列答案
相关题目
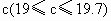 万元,商场分配给经营部的日营业额为正整数万元,问这个商场怎样分配日营业额给三个经营部?各部分别安排多少名售货员?
万元,商场分配给经营部的日营业额为正整数万元,问这个商场怎样分配日营业额给三个经营部?各部分别安排多少名售货员?