题目内容
已知数列 中,对一切自然数
中,对一切自然数 ,都有
,都有 且首项为
且首项为 ,
,
若 。
。
(1)用 表示
表示 ,并求数列
,并求数列 的通项公式;
的通项公式;
(2)若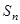 表示数列
表示数列 的前
的前 项之和,则
项之和,则 。
。
 中,对一切自然数
中,对一切自然数 ,都有
,都有 且首项为
且首项为 ,
,若
 。
。(1)用
 表示
表示 ,并求数列
,并求数列 的通项公式;
的通项公式;(2)若
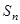 表示数列
表示数列 的前
的前 项之和,则
项之和,则 。
。(1)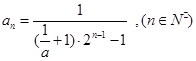 ;(2)
;(2)  。
。
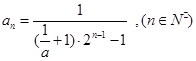 ;(2)
;(2)  。
。本试题主要是考查了递推关系式的运用以及数列求和的综合运用。
(1)因为由 ,得
,得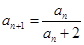 ,故
,故 ,从而得到关系式;
,从而得到关系式;
(2)由条件可得: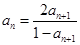 ,则
,则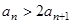 ,即
,即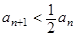 ,利用放缩法得到证明。
,利用放缩法得到证明。
解:(1)由 ,得
,得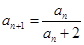 ,故
,故 ,
,
记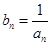 ,则
,则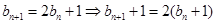 ,再记
,再记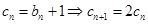 ,
,
且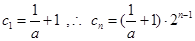 ,
,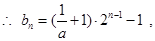
所以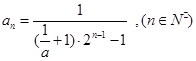
(2)由条件可得: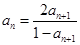 ,则
,则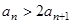 ,即
,即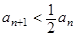
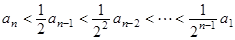 ,即
,即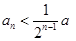 ,于是有,
,于是有,
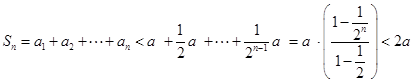 ,即
,即 。
。
(1)因为由
 ,得
,得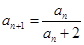 ,故
,故 ,从而得到关系式;
,从而得到关系式;(2)由条件可得:
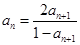 ,则
,则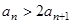 ,即
,即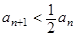 ,利用放缩法得到证明。
,利用放缩法得到证明。解:(1)由
 ,得
,得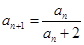 ,故
,故 ,
,记
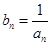 ,则
,则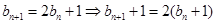 ,再记
,再记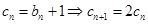 ,
,且
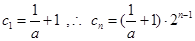 ,
,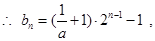
所以
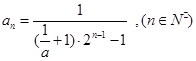
(2)由条件可得:
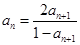 ,则
,则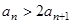 ,即
,即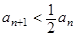
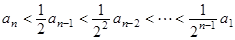 ,即
,即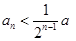 ,于是有,
,于是有,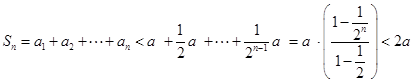 ,即
,即 。
。
练习册系列答案
相关题目




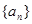 满足:
满足: 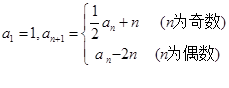
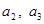 ;
; 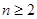 时,求
时,求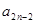 与
与 的关系式,并求数列
的关系式,并求数列 }中,
}中, 且
且 ,
, 是其前
是其前 项和,则下列判断正确的有 。
项和,则下列判断正确的有 。 ;②
;② ,
, <0;③
<0;③
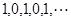 的一个通项公式是
的一个通项公式是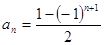
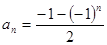
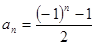
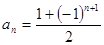
 依照以上各式的规律,得到一般性的等式为( )
依照以上各式的规律,得到一般性的等式为( )



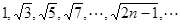 ,则
,则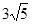 是该数列的第( )项。
是该数列的第( )项。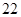

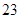

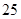

 ……,
……, (a、b为正整数)则
(a、b为正整数)则 .
.