题目内容
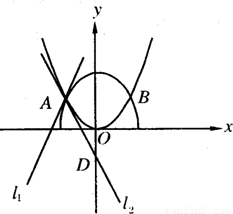
如图,曲线C1:
+
=1(b>a>0,y≥0)与抛物线C2:x2=2py(p>0)的交点分别为A,B,曲线C1与抛物线C2在点A处的切线分别为l1和l2,且斜率分别为k1和k2.
(I)k1•k2是否与p无关?若是,给出证明;若否,给以说明;
(Ⅱ)若l2与y轴的交点为D(0,-2),当a2+b2取得最小值9时,求曲线C1与抛物线C2的方程.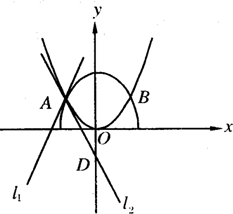
| x2 |
| a2 |
| y2 |
| b2 |
(I)k1•k2是否与p无关?若是,给出证明;若否,给以说明;
(Ⅱ)若l2与y轴的交点为D(0,-2),当a2+b2取得最小值9时,求曲线C1与抛物线C2的方程.

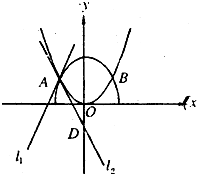
(I)设A(x0,y0),由
| x2 |
| a2 |
| y2 |
| b2 |
得y=
| b |
| a |
| a2-x2 |
| bx | ||
a
|
则k1=y′|x=x0=-
| bx0 | ||||
a
|
由x2=2py(p>0)得y=
| x2 |
| 2p |
| x0 |
| p |
所以k1k2=-
| bx0 | ||||
a
|
| x0 |
| p |
b
| ||||
pa
|
又因为
| x | 20 |
| b |
| a |
a2-
|
则
| ||
| 2p |
b
| ||||
| a |
| ||||
|
| 2pb |
| a |
代入(※)式得k1k2=-
b
| ||||
pa
|
| b |
| pa |
| 2pb |
| a |
| b |
| a |
可见,k1•k2仅与a,b有关,与p无关. …(6分)
(II)如图,设A(x0,
| ||
| 2p |
由(I)知k2=
| x0 |
| p |
| x0 |
| p |
| ||
| 2p |
又l2过点D(0,-2),则
| x | 20 |
| p |
所以A(-2
| p |
将点A的坐标代入曲线C1的方程得
| 4p |
| a2 |
| 4 |
| b2 |
则a2+b2=(a2+b2)(
| 4p |
| a2 |
| 4 |
| b2 |
| 4a2 |
| b2 |
| 4pb2 |
| a2 |
| p |
当且仅当“=”成立时,有
|
解得
|
| x2 |
| 3 |
| y2 |
| 6 |
| y |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•杨浦区二模)如图,椭圆C1:
(2012•杨浦区二模)如图,椭圆C1: (2009•枣庄一模)如图,曲线C1:
(2009•枣庄一模)如图,曲线C1: (2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.
(2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.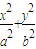 =1(b>a>0,y≥0)与抛物线C2:x2=2py(p>0)的交点分别为A,B,曲线C1与抛物线C2在点A处的切线分别为l1和l2,且斜率分别为k1和k2.
=1(b>a>0,y≥0)与抛物线C2:x2=2py(p>0)的交点分别为A,B,曲线C1与抛物线C2在点A处的切线分别为l1和l2,且斜率分别为k1和k2.