题目内容
11.(1)设a,b,c是直角三角形的三边长,其中c为斜边,且c≠1,求证:log(c+b)a+log(c-b)a=2log(c+b)a•log(c-b)a.(2)已知log${\;}_{{a}_{1}}$b1=log${\;}_{{a}_{2}}$b2=…=log${\;}_{{a}_{n}}$bn=λ,求证:log${\;}_{{a}_{1}{a}_{2}…{a}_{n}}$(b1b2…bn)=λ.
分析 (1)题意,利用对数换底公式log(c+b)a=loga(c+b),log(c-b)a=loga(c-b),证明左端=右端即可;
(2)由题意可得b1=a1λ,…,bn=anλ,从而证得结合.
解答 证明:(1)由勾股定理得a2+b2=c2,即a2=c2-b2,
∴右边=2log(c+b)a•log(c-b)a=$\frac{2}{{log}_{a}(c+b){log}_{a}(c-b)}$=$\frac{{log}_{a}{a}^{2}}{{log}_{a}(c+b){log}_{a}(c-b)}$=$\frac{{log}_{a}{(c}^{2}-{b}^{2})}{{log}_{a}(c+b){log}_{a}(c-b)}$=$\frac{{log}_{a}(c-b)+{log}_{a}(c+b)}{{log}_{a}(c+b){log}_{a}(c-b)}$=$\frac{1}{{log}_{a}(c+b)}$+$\frac{1}{{log}_{a}(c-b)}$=log(c+b)a+log(c-b)a=左边,
∴原等式成立;
(2)∵log${\;}_{{a}_{1}}$b1=log${\;}_{{a}_{2}}$b2=…=log${\;}_{{a}_{n}}$bn=λ,
∴b1=a1λ,…,bn=anλ,
∴b1b2…bn=a1λ•…•anλ=(a1a2a3…an)λ,
∴log${\;}_{{a}_{1}{a}_{2}…{a}_{n}}$(b1b2…bn)=λ.
点评 本题考查对数换底公与对数运算性质的应用,考查正向思维与逆向思维的综合应用,考查推理证明与运算能力,属于中档题

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
6.设x>0,函数f(x)=x•3x-318的零点,x0∈(k,k+1)(k∈N*),则k=( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
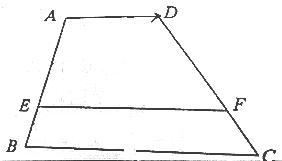 如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.
如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.