题目内容
（2012•贵阳模拟）如图所示，在长方体ABCD-A1B1C1D1中，AB=1，BC=2，CC1=5，M为棱CC1上一点．（1）若C1M=
| 3 | 2 |
（2）是否存在这样的点M使得BM⊥平面A1B1M？若存在，求出C1M的长；若不存在，请说明理由．
分析：（1）过点M作MN∥C1D，交D1D于N，连接A1N，可得∠A1MN或其补角就是异面直线A1M和C1D1所成角．再在Rt△A1NM中利用勾股定理和正切函数的定义，即可得到异面直线A1M和C1D1所成角的正切值；
（2）先假设存在M点，使得BM⊥平面A1B1M，并设C1M=x．根据平面几何知识Rt△B1MB∽Rt△MB1C1，得到B1M是B1B和C1M的比例中项，通过计算可得x=1或4，由此可知存在点M使得BM⊥平面A1B1M．
（2）先假设存在M点，使得BM⊥平面A1B1M，并设C1M=x．根据平面几何知识Rt△B1MB∽Rt△MB1C1，得到B1M是B1B和C1M的比例中项，通过计算可得x=1或4，由此可知存在点M使得BM⊥平面A1B1M．
解答：解：（1）过点M作MN∥C1D，交D1D于N，连接A1N，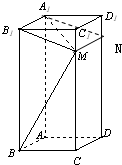
则∠A1MN或其补角就是异面直线A1M和C1D1所成角
在Rt△A1NM中，AB=1，A1N=
=
∴tan∠A1MN=
=
由此可得，当C1M=
时，异面直线A1M和C1D1所成角的正切值为
；
（2）∵A1B1⊥平面BB1C1C，BM⊆平面BB1C1C，
∴A1B1⊥BM，
因此可得：只要B1M⊥BM，就有BM⊥平面A1B1M．
假设存在M点，使得BM⊥平面A1B1M，设C1M=x
则矩形BB1C1C中，B1M⊥BM，所以∠MB1C1=∠MBB1
∴Rt△B1MB∽Rt△MB1C1，所以
=
∴B1M2=B1B•C1M，可得4+x2=5x，解之得x=1或4
∴当C1M的长为1或4时，存在点M使得BM⊥平面A1B1M．
则∠A1MN或其补角就是异面直线A1M和C1D1所成角
在Rt△A1NM中，AB=1，A1N=
22+(
|
| 5 |
| 2 |
∴tan∠A1MN=
| A1N |
| MN |
| 5 |
| 2 |
由此可得，当C1M=
| 3 |
| 2 |
| 5 |
| 2 |
（2）∵A1B1⊥平面BB1C1C，BM⊆平面BB1C1C，
∴A1B1⊥BM，
因此可得：只要B1M⊥BM，就有BM⊥平面A1B1M．
假设存在M点，使得BM⊥平面A1B1M，设C1M=x
则矩形BB1C1C中，B1M⊥BM，所以∠MB1C1=∠MBB1
∴Rt△B1MB∽Rt△MB1C1，所以
| C1M |
| B1M |
| B1M |
| B1B |
∴B1M2=B1B•C1M，可得4+x2=5x，解之得x=1或4
∴当C1M的长为1或4时，存在点M使得BM⊥平面A1B1M．
点评：本题给出特殊的四棱柱，求异面直线所成角并探索线面垂直的存在性，着重考查了异面直线所成角的求法和线面垂直的判定与性质等知识，属于中档题．
练习册系列答案
相关题目