题目内容
已知点P（1，-2）是以Q为圆心的圆Q：（x-4）2+（y-2）2=9，以PQ为直径作圆与圆Q交于A、B两点，连接PA，PB，则∠APB的余弦值为分析：根据题意求出以PQ为直径的圆的方程，利用直径所对的圆周角是直角，和解直角三角形，求得sin∠APQ=
=
，利用二倍角公式即可求得∠APB的余弦值．
| AQ |
| PQ |
| 3 |
| 5 |
解答：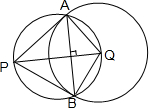
解：以PQ为直径的圆圆心为(
，0)，半径为
，
∴圆的方程为：（x-
）2+y2=
，
根据题意知AP⊥AQ，AQ=3，
∴在△PAQ中，sin∠APQ=
=
，
∴cos∠APB=cos2∠APQ=1-2sin2∠APQ=1-2×
=
，
故答案为
．
解：以PQ为直径的圆圆心为(| 5 |
| 2 |
| 5 |
| 2 |
∴圆的方程为：（x-
| 5 |
| 2 |
| 25 |
| 4 |
根据题意知AP⊥AQ，AQ=3，
∴在△PAQ中，sin∠APQ=
| AQ |
| PQ |
| 3 |
| 5 |
∴cos∠APB=cos2∠APQ=1-2sin2∠APQ=1-2×
| 9 |
| 25 |
| 7 |
| 25 |
故答案为
| 7 |
| 25 |
点评：此题考查的知识有圆周角定理，解直角三角形，以及三角函数的恒等变形等，根据题意解直角三角形是解题的关键，同时考查了学生灵活应用知识分析解决问题的能力和运算能力．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目