题目内容
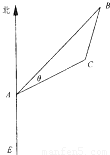
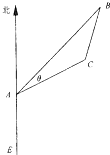 如图,有一位于A处的雷达观测站发现其北偏东45°,与A相距20
如图,有一位于A处的雷达观测站发现其北偏东45°,与A相距20| 2 |
| 1 |
| 5 |
| 13 |
(1)求该船的行驶速度v(海里/小时);
(2)在离观测站A的正南方20海里的E处有一暗礁(不考虑暗礁的面积),如果货船不改变航向继续前行,该货船是否有触礁的危险?试说明理由.
分析:(1)利用tanθ=
,0°<θ<45°,求出cosθ的值,再利用余弦定理,即可求得结论;
(2)由(1)知,在△ABC中,cosB=
,sinB=
,设BC延长线交AE于F,则∠AFB=45°-∠B,∠ACF=θ+∠B,在△AFC中,由正弦定理,即可求得结论.
| 1 |
| 5 |
(2)由(1)知,在△ABC中,cosB=
| 3 | ||
|
| 1 | ||
|
解答: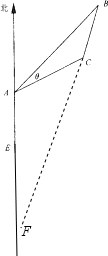 解:(1)由题意,AB=20
解:(1)由题意,AB=20
,AC=5
,∠BAC=θ
∵tanθ=
,0°<θ<45°,∴cosθ=
由余弦定理可得BC2=AB2+AC2-2AB×ACcosθ=125,∴BC=5
∵航行时间为20分钟
∴该船的行驶速度v=
=15
(海里/小时);
(2)由(1)知,在△ABC中,cosB=
=
,
∴sinB=
设BC延长线交AE于F,则∠AFB=45°-∠B,∠ACF=θ+∠B
在△AFC中,由正弦定理可得
=
∴tanθ=
,0°<θ<45°,sinθ=
,cosθ=
∴AF=
=20(海里)
∴F与E重合,即货船不改变航向继续前行会有触礁的危险.
 解:(1)由题意,AB=20
解:(1)由题意,AB=20| 2 |
| 13 |
∵tanθ=
| 1 |
| 5 |
| 5 | ||
|
由余弦定理可得BC2=AB2+AC2-2AB×ACcosθ=125,∴BC=5
| 5 |
∵航行时间为20分钟
∴该船的行驶速度v=
5
| ||
|
| 5 |
(2)由(1)知,在△ABC中,cosB=
| 800+125-325 | ||||
2×20
|
| 3 | ||
|
∴sinB=
| 1 | ||
|
设BC延长线交AE于F,则∠AFB=45°-∠B,∠ACF=θ+∠B
在△AFC中,由正弦定理可得
5
| ||
| sin(45°-B) |
| AF |
| sin(θ+B) |
∴tanθ=
| 1 |
| 5 |
| 1 | ||
|
| 5 | ||
|
∴AF=
5
| ||
| sin(45°-B) |
∴F与E重合,即货船不改变航向继续前行会有触礁的危险.
点评:本题考查正弦、余弦定理的运用,考查学生分析解决问题的能力,解题的关键是确定三角形,属于中档题.

练习册系列答案
相关题目
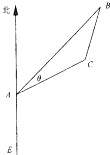 如图,有一位于A处的雷达观测站发现其北偏东45°,与A相距
如图,有一位于A处的雷达观测站发现其北偏东45°,与A相距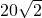 海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中
海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中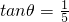 ,0°<θ<45°)且与观测站A相距
,0°<θ<45°)且与观测站A相距 海里的C处.
海里的C处.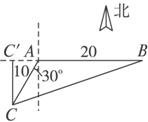
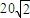 海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中
海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中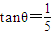 ,0°<θ<45°)且与观测站A相距
,0°<θ<45°)且与观测站A相距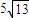 海里的C处.
海里的C处.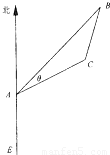
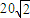 海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中
海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中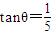 ,0°<θ<45°)且与观测站A相距
,0°<θ<45°)且与观测站A相距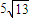 海里的C处.
海里的C处.