题目内容
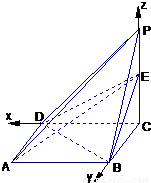
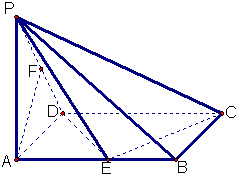
已知一四棱锥P-ABCD的三视图如图,E是侧棱PC上的动点.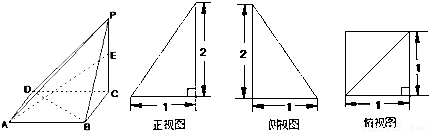
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)当点E在何位置时,BD⊥AE?证明你的结论;
(Ⅲ)若点E为PC的中点,求二面角D-AE-B的大小.
【答案】分析:(Ⅰ)由该四棱锥的三视图知,该四棱锥P-ABCD的底面是边长为1的正方形,侧棱PC⊥底面ABCD,且PC=2,由此能求出四棱锥P-ABCD的体积.
(Ⅱ)不论点E在PC上的何位置,都有BD⊥AE,欲证明证明此结论,只需证明BD⊥平面PAC,不论点E在何位置,都有AE?平面PAC即可.
(Ⅲ)法一:在平面DAE内过点D作DG⊥AE于G,连接BG,由CD=CB,EC=EC,知Rt△ECD≌Rt△ECB,故BG=EA,所以∠DGB是二面角D-EA-B的平面角,由此能求出二面角D-AE-B的大小.
法二:以点C为坐标原点,CD所在的直线为x轴建立空间直角坐标系,利用向量法能求出二面角D-AE-B的大小.
解答:解:(Ⅰ)由该四棱锥的三视图知,该四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2,
∴四棱锥P-ABCD的体积VP-ABCD=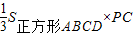 =
= .
.
(Ⅱ)不论点E在PC上的何位置,都有BD⊥AE,
证明如下:
连接AC,∵ABCD是正方形,
∴BD⊥AC,∵PC⊥底面ABCD,且BD?平面ABCD,
∴BD⊥PC,
∵AC∩PC=C,∴BD⊥平面PAC,
∵不论点E在何位置,都有AE?平面PAC,
∴不论点E在何位置,都有BD⊥AE.
(Ⅲ)解法一:在平面DAE内过点D作DG⊥AE于G,连接BG,
∵CD=CB,EC=EC,∴Rt△ECD≌Rt△ECB,
∴BG=EA,
∴∠DGB是二面角D-EA-B的平面角,
∵BC⊥DE,AD∥BC,∴AD⊥DE,
在Rt△ADE中,DG=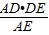 =
=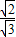 =BG,
=BG,
在△DGB中,
由余弦定理得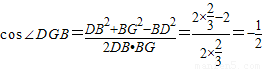
∴∠DGB=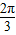 .
.
解法二:以点C为坐标原点,CD所在的直线为x轴建立空间直角坐标系如图示:
则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),从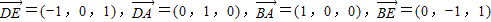
设平面ADE和平面ABE的法向量分别为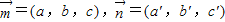
由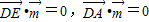 可得:-a+c=0,b=0,
可得:-a+c=0,b=0,
同理得:a'=0,-b'+c'=0.令c=1,c'=-1,则a=1,b'=-1,
∴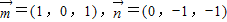 ------(10分)
------(10分)
设二面角D-AE-B的平面角为θ,则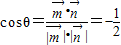
∴∠DGB=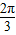 .
.
点评:本题考查四棱锥体积的求法,考查直线垂直的判断与证明,考查二面角的求法.解题时要认真审题,仔细解答,注意向量法的合理运用.
(Ⅱ)不论点E在PC上的何位置,都有BD⊥AE,欲证明证明此结论,只需证明BD⊥平面PAC,不论点E在何位置,都有AE?平面PAC即可.
(Ⅲ)法一:在平面DAE内过点D作DG⊥AE于G,连接BG,由CD=CB,EC=EC,知Rt△ECD≌Rt△ECB,故BG=EA,所以∠DGB是二面角D-EA-B的平面角,由此能求出二面角D-AE-B的大小.
法二:以点C为坐标原点,CD所在的直线为x轴建立空间直角坐标系,利用向量法能求出二面角D-AE-B的大小.
解答:解:(Ⅰ)由该四棱锥的三视图知,该四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2,
∴四棱锥P-ABCD的体积VP-ABCD=
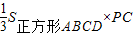 =
= .
.(Ⅱ)不论点E在PC上的何位置,都有BD⊥AE,
证明如下:
连接AC,∵ABCD是正方形,
∴BD⊥AC,∵PC⊥底面ABCD,且BD?平面ABCD,
∴BD⊥PC,
∵AC∩PC=C,∴BD⊥平面PAC,
∵不论点E在何位置,都有AE?平面PAC,
∴不论点E在何位置,都有BD⊥AE.
(Ⅲ)解法一:在平面DAE内过点D作DG⊥AE于G,连接BG,
∵CD=CB,EC=EC,∴Rt△ECD≌Rt△ECB,
∴BG=EA,
∴∠DGB是二面角D-EA-B的平面角,
∵BC⊥DE,AD∥BC,∴AD⊥DE,
在Rt△ADE中,DG=
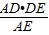 =
=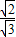 =BG,
=BG,在△DGB中,
由余弦定理得
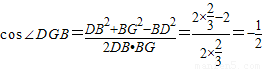
∴∠DGB=
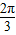 .
.解法二:以点C为坐标原点,CD所在的直线为x轴建立空间直角坐标系如图示:
则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),从
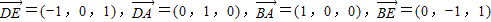
设平面ADE和平面ABE的法向量分别为
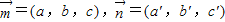
由
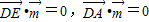 可得:-a+c=0,b=0,
可得:-a+c=0,b=0,同理得:a'=0,-b'+c'=0.令c=1,c'=-1,则a=1,b'=-1,
∴
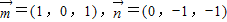 ------(10分)
------(10分)设二面角D-AE-B的平面角为θ,则
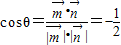
∴∠DGB=
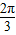 .
.
点评:本题考查四棱锥体积的求法,考查直线垂直的判断与证明,考查二面角的求法.解题时要认真审题,仔细解答,注意向量法的合理运用.

练习册系列答案
相关题目
 已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD, 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点. (2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点.
(2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点. (2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,PA=AD=1,E,F分别是AB、PD的中点.
(2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,PA=AD=1,E,F分别是AB、PD的中点.