题目内容
如图,已知椭圆C: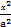 +y2=1(a>1)的上顶点为A,离心率为
+y2=1(a>1)的上顶点为A,离心率为 ,若不过点A的动直线l与椭圆C相交于P,Q两点,且
,若不过点A的动直线l与椭圆C相交于P,Q两点,且 ·
· =0.
=0.

(1)求椭圆C的方程.
(2)求证:直线l过定点,并求出该定点N的坐标.
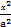 +y2=1(a>1)的上顶点为A,离心率为
+y2=1(a>1)的上顶点为A,离心率为 ,若不过点A的动直线l与椭圆C相交于P,Q两点,且
,若不过点A的动直线l与椭圆C相交于P,Q两点,且 ·
· =0.
=0.
(1)求椭圆C的方程.
(2)求证:直线l过定点,并求出该定点N的坐标.
(1) 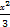 +y2=1 (2)见解析
+y2=1 (2)见解析
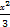 +y2=1 (2)见解析
+y2=1 (2)见解析(1)依题意有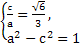 ⇒
⇒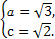
故椭圆C的方程为: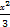 +y2=1.
+y2=1.
(2)由 ·
· =0,知AP⊥AQ,从而直线AP与坐标轴不垂直,由A(0,1)可设直线AP的方程为y=kx+1,直线AQ的方程为y=-
=0,知AP⊥AQ,从而直线AP与坐标轴不垂直,由A(0,1)可设直线AP的方程为y=kx+1,直线AQ的方程为y=- x+1(k≠0).
x+1(k≠0).
将y=kx+1代入椭圆C的方程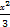 +y2=1并整理得:(1+3k2)x2+6kx=0,
+y2=1并整理得:(1+3k2)x2+6kx=0,
解得x=0或x=-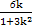 ,
,
因此P的坐标为(-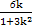 ,-
,-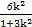 +1),
+1),
即(-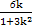 ,
,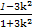 ),
),
将上式中的k换成- ,得Q(
,得Q(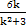 ,
,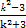 ).
).
直线l的方程为y=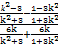 (x-
(x-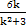 )+
)+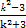 ,化简得直线l的方程为y=
,化简得直线l的方程为y=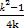 x-
x- ,
,
因此直线l过定点N(0,- ).
).
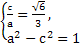 ⇒
⇒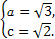
故椭圆C的方程为:
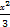 +y2=1.
+y2=1.(2)由
 ·
· =0,知AP⊥AQ,从而直线AP与坐标轴不垂直,由A(0,1)可设直线AP的方程为y=kx+1,直线AQ的方程为y=-
=0,知AP⊥AQ,从而直线AP与坐标轴不垂直,由A(0,1)可设直线AP的方程为y=kx+1,直线AQ的方程为y=- x+1(k≠0).
x+1(k≠0).将y=kx+1代入椭圆C的方程
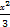 +y2=1并整理得:(1+3k2)x2+6kx=0,
+y2=1并整理得:(1+3k2)x2+6kx=0,解得x=0或x=-
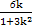 ,
,因此P的坐标为(-
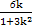 ,-
,-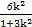 +1),
+1),即(-
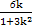 ,
,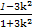 ),
),将上式中的k换成-
 ,得Q(
,得Q(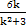 ,
,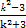 ).
).直线l的方程为y=
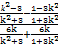 (x-
(x-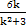 )+
)+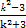 ,化简得直线l的方程为y=
,化简得直线l的方程为y=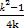 x-
x- ,
,因此直线l过定点N(0,-
 ).
).
练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+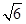 =0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
=0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点. ·
· 的取值范围;
的取值范围;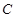 :
: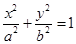
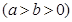 的离心率
的离心率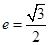 ,原点到过点
,原点到过点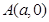 ,
,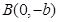 的直线的距离是
的直线的距离是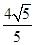 .
.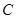 的方程;
的方程; 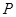
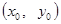 关于直线
关于直线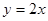 的对称点为
的对称点为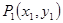 ,求
,求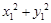 的取值范围;
的取值范围;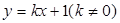 交椭圆
交椭圆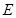 ,
,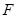 ,且
,且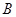 为圆心的圆上,求
为圆心的圆上,求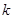 的值.
的值. 、
、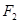 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点.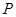 是第一象限内该椭圆上的一点,
是第一象限内该椭圆上的一点, ,求点
,求点 的直线
的直线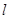 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且
,且 为锐角(其
为锐角(其 为坐标原点),求直线
为坐标原点),求直线 的取值范围.
的取值范围. 的焦点为F,过F作直线交抛物线于A、B两点,设
的焦点为F,过F作直线交抛物线于A、B两点,设 则
则 ( )
( ) D.1
D.1 ,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点. =1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
=1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.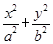 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4 .
. +
+ =t
=t (O为坐标原点),当|
(O为坐标原点),当| -
- |<
|< 时,求实数t的取值范围.
时,求实数t的取值范围.