题目内容
已知椭圆C: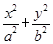 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4 .
.
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆上一点,且满足 +
+ =t
=t (O为坐标原点),当|
(O为坐标原点),当| -
- |<
|< 时,求实数t的取值范围.
时,求实数t的取值范围.
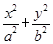 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4 .
.(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆上一点,且满足
 +
+ =t
=t (O为坐标原点),当|
(O为坐标原点),当| -
- |<
|< 时,求实数t的取值范围.
时,求实数t的取值范围.(1)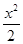 +y2=1.(2)
+y2=1.(2) ∪
∪ .
.
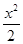 +y2=1.(2)
+y2=1.(2) ∪
∪ .
.(1)由题意知椭圆的离心率e=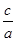 =
= ,∴e2=
,∴e2= =
= =
= ,即a2=2b2.
,即a2=2b2.
又△EGF2的周长为4 ,即4a=4
,即4a=4 ,∴a2=2,b2=1.
,∴a2=2,b2=1.
∴椭圆C的方程为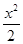 +y2=1.
+y2=1.
(2)由题意知直线AB的斜率存在,即t≠0.
设直线AB的方程为y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),由 ,
,
得(1+2k2)x2-8k2x+8k2-2=0.
由Δ=64k4-4(2k2+1)(8k2-2)>0,得k2< .
.
x1+x2= ,x1x2=
,x1x2= ,
,
∵ +
+ =t
=t ,∴(x1+x2,y1+y2)=t(x,y),x=
,∴(x1+x2,y1+y2)=t(x,y),x= =
=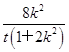 ,y=
,y= =
= [k(x1+x2)-4k]=
[k(x1+x2)-4k]=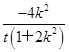 .
.
∵点P在椭圆C上,∴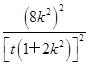 +2
+2 =2,
=2,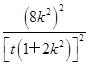
∴16k2=t2(1+2k2).
∵| -
- |<
|< ,∴
,∴ |x1-x2|<
|x1-x2|< ,
,
∴(1+k2)[(x1+x2)2-4x1x2]< ,
,
∴(1+k2) <
< ,
,
∴(4k2-1)(14k2+13)>0,∴k2> .
.
∴ <k2<
<k2< .∵16k2=t2(1+2k2),∴t2=
.∵16k2=t2(1+2k2),∴t2= =8-
=8- ,
,
又 <1+2k2<2,∴
<1+2k2<2,∴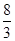 <t2=8-
<t2=8- <4,
<4,
∴-2<t<- 或
或 <t<2,
<t<2,
∴实数t的取值范围为 ∪
∪ .
.
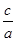 =
= ,∴e2=
,∴e2= =
= =
= ,即a2=2b2.
,即a2=2b2.又△EGF2的周长为4
 ,即4a=4
,即4a=4 ,∴a2=2,b2=1.
,∴a2=2,b2=1.∴椭圆C的方程为
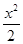 +y2=1.
+y2=1.(2)由题意知直线AB的斜率存在,即t≠0.
设直线AB的方程为y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),由
 ,
,得(1+2k2)x2-8k2x+8k2-2=0.
由Δ=64k4-4(2k2+1)(8k2-2)>0,得k2<
 .
.x1+x2=
 ,x1x2=
,x1x2= ,
,∵
 +
+ =t
=t ,∴(x1+x2,y1+y2)=t(x,y),x=
,∴(x1+x2,y1+y2)=t(x,y),x= =
=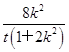 ,y=
,y= =
= [k(x1+x2)-4k]=
[k(x1+x2)-4k]=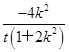 .
.∵点P在椭圆C上,∴
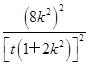 +2
+2 =2,
=2,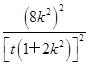
∴16k2=t2(1+2k2).
∵|
 -
- |<
|< ,∴
,∴ |x1-x2|<
|x1-x2|< ,
,∴(1+k2)[(x1+x2)2-4x1x2]<
 ,
,∴(1+k2)
 <
< ,
,∴(4k2-1)(14k2+13)>0,∴k2>
 .
.∴
 <k2<
<k2< .∵16k2=t2(1+2k2),∴t2=
.∵16k2=t2(1+2k2),∴t2= =8-
=8- ,
,又
 <1+2k2<2,∴
<1+2k2<2,∴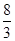 <t2=8-
<t2=8- <4,
<4,∴-2<t<-
 或
或 <t<2,
<t<2,∴实数t的取值范围为
 ∪
∪ .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 到两个定点
到两个定点 、
、 的距离之和为
的距离之和为 ,线段
,线段 的长为
的长为 .
.
 的方程;
的方程; 与轨迹
与轨迹 两点,且点
两点,且点 的垂直平分线为
的垂直平分线为 .
. 的面积的最大值;
的面积的最大值; 、
、 关于直线
关于直线 ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 的直线交椭圆
的直线交椭圆 ,
, 两点,
两点,  的距离为
的距离为 ,连接椭圆
,连接椭圆 .
. ,设
,设 是椭圆
是椭圆 两点的直线
两点的直线 交
交 轴于点
轴于点 ,若
,若 , 求
, 求 的取值范围;
的取值范围; 与椭圆
与椭圆 ,
, ,其中
,其中 ,若点
,若点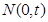 是线段
是线段 垂直平分线上一点,且满足
垂直平分线上一点,且满足 ,求实数
,求实数 的值.
的值.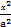 +y2=1(a>1)的上顶点为A,离心率为
+y2=1(a>1)的上顶点为A,离心率为 ,若不过点A的动直线l与椭圆C相交于P,Q两点,且
,若不过点A的动直线l与椭圆C相交于P,Q两点,且 ·
· =0.
=0.
 与
与 的离心率相等. 直线
的离心率相等. 直线 与曲线
与曲线 交于
交于 两点(
两点( 在
在 的左侧),与曲线
的左侧),与曲线 交于
交于 两点(
两点( 在
在 的左侧),
的左侧), 为坐标原点,
为坐标原点, .
. =
= ,
, 时,求椭圆
时,求椭圆 的方程;
的方程; ,且
,且 和
和 相似,求
相似,求 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,
=1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,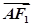 ·
· =0,3|
=0,3| |·|
|·| |=-5
|=-5 ·
· =
= ·
· ?若存在,求出实数m的取值范围;若不存在,说明理由.
?若存在,求出实数m的取值范围;若不存在,说明理由. 是椭圆
是椭圆 的左、右顶点,椭圆
的左、右顶点,椭圆 的离心率为
的离心率为 ,右准线
,右准线 的方程为
的方程为 .
.
 是椭圆
是椭圆 交
交 ,以
,以 为直径的圆记为
为直径的圆记为 . ①若
. ①若 所得的弦长;
所得的弦长; 交于点
交于点 ,试证明:直线
,试证明:直线 与
与 轴的交点
轴的交点 为定点,并求该定点的坐标.
为定点,并求该定点的坐标. .
. 轴上,焦距为2,直线n:x-y-1=0与椭圆C交于A、B两点,F1是左焦点,且
轴上,焦距为2,直线n:x-y-1=0与椭圆C交于A、B两点,F1是左焦点,且 ,则椭圆C的标准方程是
,则椭圆C的标准方程是