题目内容
(
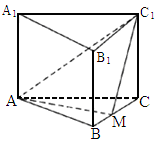
唐山一中模拟)如下图所示,正三棱柱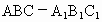 的底面边长为a,点M在BC上,△
的底面边长为a,点M在BC上,△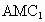 是以点M为直角顶点的等腰直角三角形.
是以点M为直角顶点的等腰直角三角形.
(1)
求证:点M为边BC的中点;(2)
求点C到平面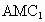 的距离;
的距离;
(3)
求二面角 的大小.
的大小.
答案:略
解析:
解析:
|
解析: (1)证明:∵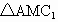 是以点M为直角顶点的等腰直角三角形, 是以点M为直角顶点的等腰直角三角形,
∴ AM⊥ 且AM= 且AM=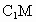 . .
∵正三棱柱 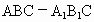 , ,
∴  ⊥底面ABC. ⊥底面ABC.
∴  在底面内的射影为CM,AM⊥CM. 在底面内的射影为CM,AM⊥CM.
∵底面 ABC是边长为a的正三角形,∴点 M为BC边的中点.(2) 过点C作 , ,
由 (1)知 , ,
∴ AM⊥平面 . .
∵ CH在平面 内,∴CH⊥AM, 内,∴CH⊥AM,
∴ CH⊥平面 , ,
由 (1)知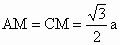 , ,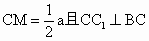 , ,
∴  . .
∴  . .
∴点 C到平面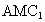 的距离为 的距离为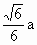 . .
(3) 过点C作CI⊥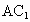 于I,连HI, 于I,连HI,
CH ⊥平面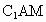 , ,
∴ HI为CI在平面 内的射影, 内的射影,
∴ HI⊥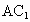 ,∠CIH是二面角 ,∠CIH是二面角 的平面角. 的平面角.
在直角三角形 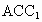 中, 中,
 , ,
∴∠ CIH=45°.∴二面角  的大小为45°. 的大小为45°. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(2007
北京宣武模拟)如下图所示,正方体 中,E、F分别是正方形
中,E、F分别是正方形 和ABCD的中心,G是
和ABCD的中心,G是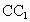 的中点,设GF、
的中点,设GF、 与AB所成的角分别为α、β,则α+β等于
与AB所成的角分别为α、β,则α+β等于

[
]|
A .120° |
B .60° |
C .75° |
D .90° |


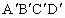 中,棱长为1,E、F分别是BC、CD上的点,且BE=CF=a(0<a<1),则
中,棱长为1,E、F分别是BC、CD上的点,且BE=CF=a(0<a<1),则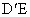 与
与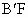 的位置关系是
的位置关系是
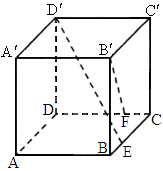
 中,点E为棱
中,点E为棱 的动点.
的动点.
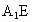 ⊥BD;
⊥BD;
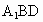 ⊥平面EBD;
⊥平面EBD;
 —BD—E的大小为45°?如果存在,试确定点E在棱
—BD—E的大小为45°?如果存在,试确定点E在棱 上的位置;如果不存在,请说明理由.
上的位置;如果不存在,请说明理由.
