Question

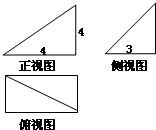
某几何体的三视图如图所示，当a+b取最大值时，该几何体的表面积是

2

2

+1

．

Answer 1

分析：由三视图及题设条件知，此几何体为一个三棱锥，底面一边长为1的直角三角形，一条棱长为2，由于本题中含有两个参数，且需求满足两者和最大时的体积，故本题第一步是找到关于a，b的表达式，先求其和最大时两参数的值，再由体积公式求体积，观察发现，可以先用参数a，b表示出PC，PB的值，在直角三角形BPC中用公股定理建立关于a，b的方程，研究此方程求出满足条件的参数的值再求表面积即可．

解答：解：由题设可得其直观图如图，
由三视图知，PA，PB，PC两两垂直
PA=1，BC=2，AB=b，AC=a
如图有PC=

a2-1

，PB=

b2-1

在直角三角形BPC中有PC²+PB²=BC²=4，
即a²-1+b²-1=4，即a²+b²=6，
可设a=

6

cosθ，b=

6

sinθ，θ∈（0，2π）
则a+b=

6

cosθ+

6

sinθ
=2

3

sin（ θ+

π

4

）≤2

3

，
最大值当 θ=

π

4

时取到．
此时a=b=

3

，验证知符合题意．
由此知PC=

a2-1

=

2

，PB=

b2-1

=

2

，
∴S△PAB=

1

2

×1×

2

=

2

2

，
S△PAC=

1

2

×1×

2

=

2

2

，
S△PBC=

1

2

×

2

×

2

=1，
△ABC中，作AH⊥BC，交BC于H，
∵PB=PC=

3

，BC=2，
∴AH=

3-1

=

2

，
∴S△ABC=

1

2

×2×

2

=

2

．
∴几何体的表面积S=

2

2

+

2

2

+1+

2

=2

2

+1．
故答案为：2

2

+1．

点评：本题考点是由三视图求几何体的面积、体积，考查对三视图的理解与应用，主要考查三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据，再根据相关的公式求表面积与体积，本题求的是三棱锥的表面积．三视图的投影规则是：“主视、俯视 长对正；主视、左视高平齐，左视、俯视 宽相等”．三视图是新课标的新增内容，在以后的高考中有加强的可能．本题增加了最值问题的考查，题目难度增加，综合性较强．