题目内容
已知函数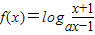
（a＞0且a≠1）．（1）求f（x）的定义域；
（2）判断f（x）的单调性，写出你的结论，不要求证明．
【答案】分析：（1）由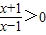
，得x＜-1或x＞1，由此能求出f（x）的定义域．
（2）由对数函数的性质知当0＜a＜1时，f（x）在（-∞，-1）和（1，+∞）上都是增函数；当a＞1时，f（x）在（-∞，-1）和（1，+∞）上都是减函数．
解答：解：（1）由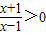
，
得x＜-1或x＞1，
∴f（x）的定义域为（-∞，-1）∪（1，+∞）．
（2）当0＜a＜1时，
f（x）在（-∞，-1）和（1，+∞）上都是增函数；
当a＞1时，
f（x）在（-∞，-1）和（1，+∞）上都是减函数．
点评：本题考查指数函数的性质和应用，解题时要认真审题，仔细解答．
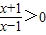，得x＜-1或x＞1，由此能求出f（x）的定义域．（2）由对数函数的性质知当0＜a＜1时，f（x）在（-∞，-1）和（1，+∞）上都是增函数；当a＞1时，f（x）在（-∞，-1）和（1，+∞）上都是减函数．
解答：解：（1）由
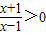，得x＜-1或x＞1，
∴f（x）的定义域为（-∞，-1）∪（1，+∞）．
（2）当0＜a＜1时，
f（x）在（-∞，-1）和（1，+∞）上都是增函数；
当a＞1时，
f（x）在（-∞，-1）和（1，+∞）上都是减函数．
点评：本题考查指数函数的性质和应用，解题时要认真审题，仔细解答．
练习册系列答案
相关题目
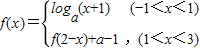（a＞0且a≠1），若x1≠x2，且f（x1）=f（x2），则x1+x2的值（ ）
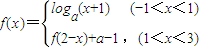（a＞0且a≠1），若x1≠x2，且f（x1）=f（x2），则x1+x2的值（ ）
（a＞0且a为常数）．
对x∈[-
，+∞）恒成立，求a的取值范围．
其中a>0,且a≠1，
的定义域；
；
恒成立，求实数m的取值范围.
=loga
(a＞0且a≠1)是奇函数
，（