题目内容
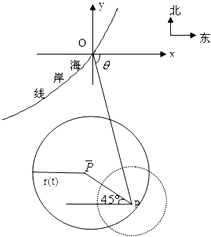 在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南θ(cosθ=
在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南θ(cosθ=
| ||
| 10 |
分析:建立坐标系:以O为原点,正东方向为x轴正向.设在时刻:t(h)台风中心P(x,y)的坐标进而可知此时台风侵袭的区域,根据题意可知其中r(t)=10t+60,若在t时,该城市O受到台风的侵袭,则有(0-x)2+(0-y)2≤(10t+60)2,进而可得关于t的一元二次不等式,求得t的范围,答案可得.
解答:解:如图建立坐标系:以O为原点,正东方向为x轴正向.
在时刻:t(h)台风中心P(x,y)的坐标为
令(x′,y′)是台风边缘线上一点,则此时台风侵袭的区域是(x′-x)2+(y′-y)2≤[r(t)]2,
其中r(t)=10t+60,
若在t时,该城市受到台风的侵袭,
则有(0-x)2+(0-y)2≤(10t+60)2,
即(300×
-20×
t)2+(-300×
+20×
t)2≤(10t+60)2,
即t2-36t+288≤0,解得12≤t≤24.
答:12小时后该城市开始受到台风气侵袭.
在时刻:t(h)台风中心P(x,y)的坐标为
|
令(x′,y′)是台风边缘线上一点,则此时台风侵袭的区域是(x′-x)2+(y′-y)2≤[r(t)]2,
其中r(t)=10t+60,
若在t时,该城市受到台风的侵袭,
则有(0-x)2+(0-y)2≤(10t+60)2,
即(300×
| ||
| 10 |
| ||
| 2 |
7
| ||
| 10 |
| ||
| 2 |
即t2-36t+288≤0,解得12≤t≤24.
答:12小时后该城市开始受到台风气侵袭.
点评:本题主要考查了圆的方程的综合运用.考查了学生运用所学知识解决实际问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南
在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南 

 方向300 km的海面P处,并以20 km
/ h的速度向西偏北
方向300 km的海面P处,并以20 km
/ h的速度向西偏北 的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?
的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?