题目内容
((本小题满分12分)
如图,四棱锥S—ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB= .
.

(Ⅰ)求面ASD与面BSC所成二面角的大小;
(Ⅱ)设棱SA的中点为M,求异面直线DM与
SB所成角的大小;
(Ⅲ)求点D到平面SBC的距离.
【答案】
(本小题满分12分)
证明:(Ⅰ)∵SD⊥底面ABCD,ABCD是正方形,∴CD⊥平面SAD,AD⊥平面SDC,又在Rt△SDB中,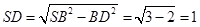 .……1分
.……1分
以D为坐标原点,DA为x轴,DC为y轴,DS为z轴,建立空间直角坐标系,则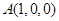 ,
,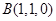 ,
,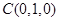 ,
,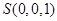 .
…………2分
.
…………2分
设平面SBC的法向量为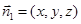 ,则
,则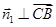 ,
,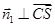 ,
,
∵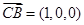 ,
,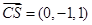 ,∴
,∴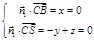 ,∴可取
,∴可取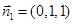 …4分
…4分
∵CD⊥平面SAD,∴平面SAD的法向量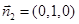 .
……………5分
.
……………5分
∴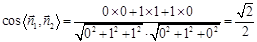 ,∴面ASD与面BSC所成二面角的大小为45°.……6分
,∴面ASD与面BSC所成二面角的大小为45°.……6分
(Ⅱ)∵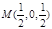 ,∴
,∴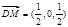 ,
,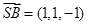 ,又∵
,又∵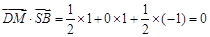 ,
,
∴DM⊥SB, ∴异面直线DM与SB所成角的大小为90°. ………9分
(Ⅲ)由(Ⅰ)平面SBC的法向量为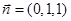 ,∵
,∵ ,
,
∴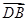 在
在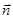 上的射影为
上的射影为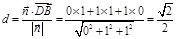 ,∴点D到平面SBC的距离为
,∴点D到平面SBC的距离为 .………12分
.………12分
【解析】略

练习册系列答案
相关题目