题目内容
(2013•德州二模)已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,
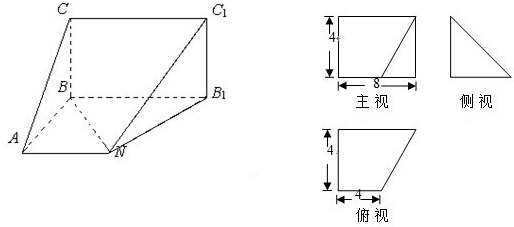
(1)求证:BC∥平面C1B1N;
(2)求证:BN⊥平面C1B1N;
(3)求此几何体的体积.

(1)求证:BC∥平面C1B1N;
(2)求证:BN⊥平面C1B1N;
(3)求此几何体的体积.
分析:(1)利用几何体的三视图,判断侧面BCC1B1是矩形,利用直线与平面平行的判定定理证明BC∥平面C1B1N;
(2)该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,BA,BC,BB1两两垂直.通过计算得出∠BNB1 为直角,从而有BN⊥B1N,再根据线面垂直的判定,即可证明BN⊥平面C1B1N;
(3)连接CN,把几何体分割成一个三棱锥和一个四棱锥,即可求解.
(2)该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,BA,BC,BB1两两垂直.通过计算得出∠BNB1 为直角,从而有BN⊥B1N,再根据线面垂直的判定,即可证明BN⊥平面C1B1N;
(3)连接CN,把几何体分割成一个三棱锥和一个四棱锥,即可求解.
解答: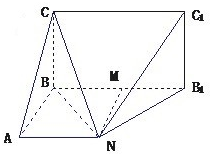 解:(1)证明:∵该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,∴BA,BC,BB1两两互相垂直.
解:(1)证明:∵该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,∴BA,BC,BB1两两互相垂直.
∵BC∥B1C1,B1C1?平面C1B1N,BC?平面C1B1N,
∴BC∥平面C1B1N…(4分)
(2)连BN,过N作NM⊥BB1,垂足为M,
∵B1C1⊥平面ABB1N,BN?平面ABB1N,
∴B1C1⊥BN,…(5分)
由三视图知,BC=4,AB=4,BM=AN=4,BA⊥AN,
∴BN=
=4
,B1N=
=
=4
,…(6分)
∵BB1=82=64,B1N2+BN2=32+32=64,
∴BN⊥B1N,…(7分)
∵B1C1?平面B1C1N,B1N?平面B1C1N,B1N∩B1C1=B1
∴BN⊥平面C1B1N …(9分)
(3)连接CN,
VC-BCN=
×BC•S△ABN=
×4×
×4×4=
…(11分)
∴平面B1C1CB⊥ANB1B=BB1,NM⊥BB1,NM?平面B1C1CB,
∴NM⊥平面B1C1CB,
V N-B1C1CB=
×NM•S 矩形B1C1CB=
×4×4×8=
…(13分)
此几何体的体积V=VC-BCN+V N-B1C1CB=
+
=32;
V=VC-BCN+V N-B1C1CB=
+
=
…(14分)
 解:(1)证明:∵该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,∴BA,BC,BB1两两互相垂直.
解:(1)证明:∵该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,∴BA,BC,BB1两两互相垂直.∵BC∥B1C1,B1C1?平面C1B1N,BC?平面C1B1N,
∴BC∥平面C1B1N…(4分)
(2)连BN,过N作NM⊥BB1,垂足为M,
∵B1C1⊥平面ABB1N,BN?平面ABB1N,
∴B1C1⊥BN,…(5分)
由三视图知,BC=4,AB=4,BM=AN=4,BA⊥AN,
∴BN=
| 42+42 |
| 2 |
| NM2+B1M2 |
| 42+42 |
| 2 |
∵BB1=82=64,B1N2+BN2=32+32=64,
∴BN⊥B1N,…(7分)
∵B1C1?平面B1C1N,B1N?平面B1C1N,B1N∩B1C1=B1
∴BN⊥平面C1B1N …(9分)
(3)连接CN,
VC-BCN=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 32 |
| 3 |
∴平面B1C1CB⊥ANB1B=BB1,NM⊥BB1,NM?平面B1C1CB,
∴NM⊥平面B1C1CB,
V N-B1C1CB=
| 1 |
| 3 |
| 1 |
| 3 |
| 128 |
| 3 |
此几何体的体积V=VC-BCN+V N-B1C1CB=
| 32 |
| 3 |
| 64 |
| 3 |
V=VC-BCN+V N-B1C1CB=
| 32 |
| 3 |
| 128 |
| 3 |
| 160 |
| 3 |
点评:本小题主要考查直线与平面的位置关系、平面与平面的位置关系、棱锥的体积等有关知识,考查空间想象能力和思维能力.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目

 (2013•德州二模)为了解某校教师使用多媒体进行教学的情况,将全校200名 教师按一学期使用多媒体进行教学的次数分成了[0,9),[10,19),[20,29),[30,39),[40,49)五层.现采用分层抽样从该校教师中抽取20名教师,调查了他们上学期使用多媒体进行教学的次数,结果用茎叶图表示如图,据此可知该校一学期使用多媒体进行教学的次数在[30,39)内的教师人数为
(2013•德州二模)为了解某校教师使用多媒体进行教学的情况,将全校200名 教师按一学期使用多媒体进行教学的次数分成了[0,9),[10,19),[20,29),[30,39),[40,49)五层.现采用分层抽样从该校教师中抽取20名教师,调查了他们上学期使用多媒体进行教学的次数,结果用茎叶图表示如图,据此可知该校一学期使用多媒体进行教学的次数在[30,39)内的教师人数为