题目内容
（09年山东猜题卷）已知函数
求：
（I）求证：函数
的图象关于点
中心对称，并求
的值；
（II）设
，且1＜a1＜2，求证
+…+
＜2.
解析：（I）设P（1
）是函数
的图象上的任一点，则
，又
关于
的对称点是
，………………………（1分）
而
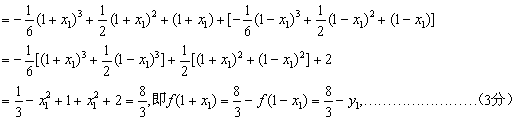
点
也在函数的图象上，故的图象关于点
中心对称. …(4分)
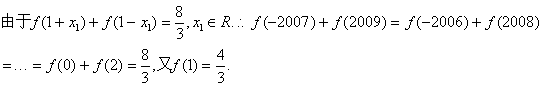
…………………………（6分）
（II）由于
.…………（7分）
＜
＜2，∴1＜
＜
，同理可得，1＜
＜，猜想1＜
＜（
）.……………………（8分）
下面用数学归纳法证明：（1）当n=2时，前面已证：
（2）假设当
1＜
＜则
，又
在
上单调递减，
＜
＜
=
=，这说明
时，命题也成立.
综上（1）（2）可知1＜＜
.……………………………（10分）
又
由于1＜＜，∴
＜1，∴
＜
，
于是
＜
＜…＜
＜
（
）（12分）
所以，
+
+…+
＜1+
＜2…（13分）
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
；
上任一点
向
轴作垂线，垂足为
，点
分
所成的比为
。问：点
的斜率为
，且过点
，直线
，
两点，又
，求曲线
设向量
的取值范围;
试确定实数
的取值范围.
的前
项和为
，且
是
中，
，点
在直线
上。
和
的值；
的通项
；
，求数列
的前n项和
。
上变化，求x的变化范围；
所成的角.