题目内容
下列命题:①偶函数的图象一定与y轴相交;
②定义在R上的奇函数f(x)必满足f(0)=0;
③f(x)=(2x+1)2-2(2x-1)既不是奇函数又不是偶函数;
④A=R,B=R,f:x→y=
| 1 |
| x+1 |
⑤f(x)=
| 1 |
| x |
其中真命题的序号是
分析:对于命题①④⑤举一个反例,说明命题不正确;对于命题②用奇函数的定义证明;对于命题③利用偶函数定义证明.
解答:解:例如f(x)=
是偶函数但不与y轴相交,故①错;
若f(x)为奇函数,所以有f(-0)=-f(0),所有f(0)=0,故②正确;
∵f(x)=(2x+1)2-2(2x-1)=4x2+3,∴f(-x)=4(-x)2+3=4x2+3=f(x)
∴f(x)为偶函数,故③错;
∵-1∈A,但按对应法则f:x→y=
B中无元素与之对应,故④错;
例如x=-1时f(-1)=-1;x=2时,f(2)=
,有f(-1)<f(2),故⑤错
故答案为②
| 1 |
| x2 |
若f(x)为奇函数,所以有f(-0)=-f(0),所有f(0)=0,故②正确;
∵f(x)=(2x+1)2-2(2x-1)=4x2+3,∴f(-x)=4(-x)2+3=4x2+3=f(x)
∴f(x)为偶函数,故③错;
∵-1∈A,但按对应法则f:x→y=
| 1 |
| x+1 |
例如x=-1时f(-1)=-1;x=2时,f(2)=
| 1 |
| 2 |
故答案为②
点评:本题考查奇函数、偶函数定义;映射定义;单调性的定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 轴相交; ②定义在
轴相交; ②定义在 上的奇函数
上的奇函数 必满足
必满足 ;
; 既不是奇函数又不是偶函数;
既不是奇函数又不是偶函数; ,则
,则 为
为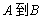 的映射;
的映射; 在
在 上是减函数.
上是减函数.