题目内容
下列命题:①偶函数的图象一定与y轴相交;
②定义在R上的奇函数f(x)必满足f(0)=0;
③幂函数f(x)=
| 1 | x |
④函数y=ax-5+1(a>0且a≠1)的图象必经过定点(5,1);
⑤函数y=log2(kx2+kx+1)的定义域为R,则实数k的范围为0<k<4.
其中真命题的序号是
分析:①可以举例说明不正确.②由奇函数定义推导.③单调区间不能合并,不正确.④函数y=ax-5+1(a>0且a≠1)的图象必经过定点(5,2)⑤函数y=log2(kx2+kx+1)的定义域为R,转化为kx2+kx+1>0,x∈R恒成立,用判别式法求解判断.
解答:解:①偶函数的图象不一定与y轴相交,如y=x-2;所以不正确.
②定义在R上的奇函数,则有f(-0)=-f(0),所以f(0)=0;所以正确.
③幂函数f(x)=
在(-∞,0)∪(0,+∞)上是减函数;单调区间不能合并,所以不正确.
④函数y=ax-5+1(a>0且a≠1)的图象必经过定点(5,2),所以不正确;
⑤函数y=log2(kx2+kx+1)的定义域为R,
则kx2+kx+1>0,x∈R恒成立
当k=0时,成立
当k>0时,△=k2-4k<0
解得:0<k<4
综上:0≤k<4
所以不正确.
故答案为:②
②定义在R上的奇函数,则有f(-0)=-f(0),所以f(0)=0;所以正确.
③幂函数f(x)=
| 1 |
| x |
④函数y=ax-5+1(a>0且a≠1)的图象必经过定点(5,2),所以不正确;
⑤函数y=log2(kx2+kx+1)的定义域为R,
则kx2+kx+1>0,x∈R恒成立
当k=0时,成立
当k>0时,△=k2-4k<0
解得:0<k<4
综上:0≤k<4
所以不正确.
故答案为:②
点评:本题主要考查奇偶函数的图象和定义,常见的图象和性质以及不等式恒成立问题,考查面广,涉及知识点多,这类题要求学习要扎实,细致,用心.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 轴相交; ②定义在
轴相交; ②定义在 上的奇函数
上的奇函数 必满足
必满足 ;
; 既不是奇函数又不是偶函数;
既不是奇函数又不是偶函数; ,则
,则 为
为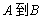 的映射;
的映射; 在
在 上是减函数.
上是减函数.