题目内容
(本题满分12分)
已知f(x)=6co s2x-2
s2x-2 sinxcosx-3.
sinxcosx-3.
(1)求f(x)的值域及最小正周期;
(2)设锐角△ABC的内角A、B满足f (A)=2f(B)=-2
(A)=2f(B)=-2 ,AB=
,AB= ,求B、C.
,求B、C.
已知f(x)=6co
 s2x-2
s2x-2 sinxcosx-3.
sinxcosx-3.(1)求f(x)的值域及最小正周期;
(2)设锐角△ABC的内角A、B满足f
 (A)=2f(B)=-2
(A)=2f(B)=-2 ,AB=
,AB= ,求B、C.
,求B、C.解:(1)f(x)=3(1+cos2x)- sin2x-3
sin2x-3
=2 (
( )
)
=2 cos(2x+
cos(2x+ )………………
)……………… ……………………………3分
……………………………3分
f(x)的值域为[-2 ,2
,2 ],周期为π; ……………………4分
],周期为π; ……………………4分
(2)由f(A)=2 cos(2A+
cos(2A+ )=-2
)=-2 得cos(2A+
得cos(2A+ )=-1,
)=-1,
∵0<A< ,
, <
< 2A+
2A+ <
< ,
,
∴2A+ =π,A=
=π,A=
 ……………………………………………6分
……………………………………………6分
由f(B)=2 cos(2B+
cos(2B+ )=-
)=- 得cos(2B+
得cos(2B+ )=-
)=- ,
,
∵0<B< ,
, <2B+
<2B+ <
< ,
,
∴2B+ =
= ,B=
,B= .
.
因此C=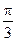 . ………………………………………………………9分
. ………………………………………………………9分
根据正弦定理得 =2,
=2,
所以BC=2sinA=2sin( +
+ )=
)= . ……………………12分
. ……………………12分
 sin2x-3
sin2x-3=2
 (
( )
)=2
 cos(2x+
cos(2x+ )………………
)……………… ……………………………3分
……………………………3分f(x)的值域为[-2
 ,2
,2 ],周期为π; ……………………4分
],周期为π; ……………………4分(2)由f(A)=2
 cos(2A+
cos(2A+ )=-2
)=-2 得cos(2A+
得cos(2A+ )=-1,
)=-1,∵0<A<
 ,
, <
< 2A+
2A+ <
< ,
,∴2A+
 =π,A=
=π,A=
 ……………………………………………6分
……………………………………………6分由f(B)=2
 cos(2B+
cos(2B+ )=-
)=- 得cos(2B+
得cos(2B+ )=-
)=- ,
,∵0<B<
 ,
, <2B+
<2B+ <
< ,
,∴2B+
 =
= ,B=
,B= .
.因此C=
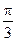 . ………………………………………………………9分
. ………………………………………………………9分根据正弦定理得
 =2,
=2,所以BC=2sinA=2sin(
 +
+ )=
)= . ……………………12分
. ……………………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,如果
中,如果
 则
则 的大小是 ( )
的大小是 ( )

 或
或
 中,已知
中,已知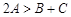 且
且 ,则
,则 的范围是( )
的范围是( )



 ,那么
,那么
 .
. ,对着山峰在平行地面上前进600m后测仰角为原来的2倍,继续在平行地面上前进200
,对着山峰在平行地面上前进600m后测仰角为原来的2倍,继续在平行地面上前进200 后,测得山峰的仰角为原来的4倍,则该山峰的高度是( )
后,测得山峰的仰角为原来的4倍,则该山峰的高度是( )

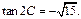
 的值;(2)当
的值;(2)当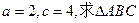 的面积。
的面积。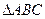 中,
中,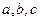 分别是角
分别是角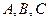 的对边,且有
的对边,且有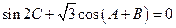 .若
.若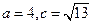 ,
,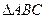 中,
中,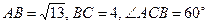 ,则
,则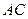 的长等于__________________.
的长等于__________________.