题目内容
在 中,如果
中,如果
 则
则 的大小是 ( )
的大小是 ( )
 中,如果
中,如果
 则
则 的大小是 ( )
的大小是 ( )A. | B. | C. 或 或 | D. 或 或 |
A
把题设等式分别平方后,相加,然后利用同角三角函数的基本关系和二倍角公式求得sin(A+B)的值,进而求得sinC的值,即可求出结果.
解:∵4sinA+2cosB=1,2sinB+4cosA=3 ,
,
∴16sin2A+4cos2B+16sinAcosB=1,①
4sin2B+16cos2A+16sinBcosA=27②
①+②得16+4+16sin(A+B)=28,
∴sin(A+B)=sin(π-C)=sinC=
得出∠C= 或
或  ,
,
若C= ,则A+B=
,则A+B=  ,4cosA<4,2sinB<1,2sinB+4cosA=3
,4cosA<4,2sinB<1,2sinB+4cosA=3 ,不成立,
,不成立,
所以C=
故答案选A
解:∵4sinA+2cosB=1,2sinB+4cosA=3
 ,
,∴16sin2A+4cos2B+16sinAcosB=1,①
4sin2B+16cos2A+16sinBcosA=27②
①+②得16+4+16sin(A+B)=28,
∴sin(A+B)=sin(π-C)=sinC=

得出∠C=
 或
或  ,
,若C=
 ,则A+B=
,则A+B=  ,4cosA<4,2sinB<1,2sinB+4cosA=3
,4cosA<4,2sinB<1,2sinB+4cosA=3 ,不成立,
,不成立,所以C=

故答案选A

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是等边三角形,
是等边三角形, ,
, ,
, 三点共线,
三点共线,
 的值;
的值; 的长.
的长. s2x-2
s2x-2 sinxcosx-3.
sinxcosx-3. (A)=2f(B)=-2
(A)=2f(B)=-2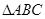 中,角
中,角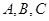 的对边分别是
的对边分别是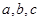 ,下列命题:
,下列命题: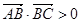 ,则△ABC为钝角三角形。
,则△ABC为钝角三角形。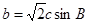 ,则C=45º.
,则C=45º.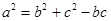 ,则
,则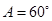 .
.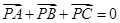 ,设
,设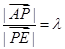 ,则
,则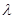 =2,其中正确命题的个数是
=2,其中正确命题的个数是 中,下列命题中正确的是 ( )
中,下列命题中正确的是 ( ) ,则
,则
 ,则
,则
 ,
, ,
, 的三角形有一解
的三角形有一解  ,
, ,
, 的三角形一定存在
的三角形一定存在 ,
,  ,则
,则 的最大值是
的最大值是 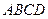 由两个正方形拼成,则
由两个正方形拼成,则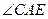 的正切值为 .
的正切值为 .
 红方一艘侦察艇发现在北偏东45°方向
红方一艘侦察艇发现在北偏东45°方向 ,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+
,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+ 方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角
方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角
 中,角
中,角 所对的边长分别为
所对的边长分别为 ,
, ,则
,则 .
.