题目内容
用直线y=m和直线y=x将区域x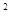 +y
+y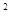
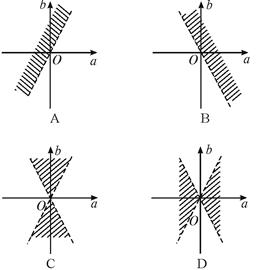
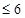 分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是
分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是
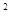 +y
+y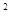
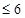 分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是
分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是A.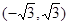 | B.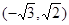 | C.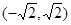 | D.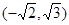 |
A
分析:由题意知Y=X与X=m两直线的交点必在Y=X这条直线上,而要想使任意两块不同色共有涂法120种,必须让直线X=m,Y=X将圆分成四块不同的面积,那么不同的涂法是5×4×3×2,要求出Y=X与圆的交点,得到结果.
解:由题意知Y=X与X=m两直线的交点必在Y=X这条直线上,
而要想使任意两块不同色共有涂法120种,
∴必须让直线X=m,Y=X将圆分成四块不同的面积,
那么不同的涂法才能是5×4×3×2=120.
要求出Y=X与圆的交点分别为(-
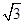 ,-
,-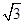 )(
)(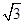 ,
,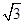 ).
).∴-
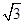 ≤m≤
≤m≤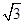 ,
,∵当m=
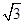 或-
或-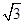 时,两直线只能把该圆分成三个区域,
时,两直线只能把该圆分成三个区域,∴不成立,
∴-
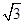 <m<
<m<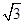 .
.故答案为:A

练习册系列答案
相关题目
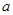 、
、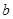 是非零实数,若
是非零实数,若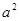 <
<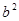
 <
<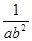 <
<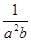
 <
<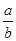
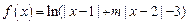 (
(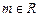 ).
).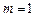 时,求函数
时,求函数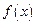 的定义域;
的定义域;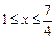 时,
时,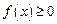 恒成立,求实数
恒成立,求实数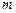 的取值范围.
的取值范围.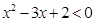 的解集为( )
的解集为( )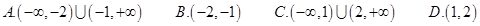
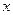 的不等式
的不等式 的解集为
的解集为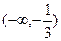 则关于
则关于 的解集为_______
的解集为_______