题目内容
已知椭圆C：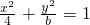
，直线l：y=mx+1，若对任意的m∈R，直线l与椭圆C恒有公共点，则实数b的取值范围是
- A.[1，4）
- B.[1，+∞）
- C.[1，4）∪（4，+∞）
- D.（4，+∞）
C
分析：把直线l：y=mx+1代入椭圆C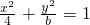：，得bx2+4（mx+1）2=4b，△=64m2-4×（b+4m2）×（4-4b）≥0，∴b≥1-4m2，再由b≠4，得到b∈[1，4）∪（4，+∞）．
解答：把直线l：y=mx+1代入椭圆C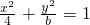：，得bx2+4（mx+1）2=4b，
整理得（b+4m2）x2+8mx+4-4b=0，△=64m2-4×（b+4m2）×（4-4b）≥0
解得16b（b-4m2+1）≥0，∵b＞0，∴b-4m2+1≥0，
∴b≥1-4m2，∵b≠4，∴b∈[1，4）∪（4，+∞）．
故选C．．
点评：本题纵使考查椭圆的性质和椭圆与直线的位置关系，解题时要注意b≠4这个条件．
分析：把直线l：y=mx+1代入椭圆C：
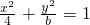，得bx2+4（mx+1）2=4b，△=64m2-4×（b+4m2）×（4-4b）≥0，∴b≥1-4m2，再由b≠4，得到b∈[1，4）∪（4，+∞）．解答：把直线l：y=mx+1代入椭圆C：
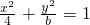，得bx2+4（mx+1）2=4b，整理得（b+4m2）x2+8mx+4-4b=0，△=64m2-4×（b+4m2）×（4-4b）≥0
解得16b（b-4m2+1）≥0，∵b＞0，∴b-4m2+1≥0，
∴b≥1-4m2，∵b≠4，∴b∈[1，4）∪（4，+∞）．
故选C．．
点评：本题纵使考查椭圆的性质和椭圆与直线的位置关系，解题时要注意b≠4这个条件．
练习册系列答案
孟建平名校考卷系列答案
相关题目
，直线l：y=ax+b（a，b∈R）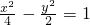
，或改为抛物线方程y2=4x，再在第（4）问添加的条件中选择一个，求出直线l的方程．
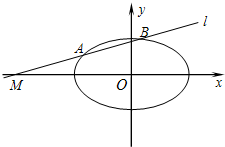已知椭圆C：
，直线l过点M（m，0）．
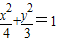，直线l过点M（m，0）．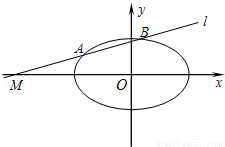
，直线l与椭圆C相交于A、B两点，
（其中O为坐标原点）．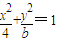
，直线l：y=mx+1，若对任意的m∈R，直线l与椭圆C恒有公共点，则实数b的取值范围是（ ）