题目内容
已知点Bn(n,yn),…(n∈N+)是某直线l上的点,以Bn为圆心作圆.所作的圆与x轴交于An和An+1两点,记An、An+1的横坐标分别为xn、xn+1.其中x1=a(0<a≤1)
(1)证明:xn+2-xn是常数,并求数列{xn}的通项公式;
(2)若l的方程为y=
x+
,试问在△AnBnAn+1(n∈N+)中是否存在直角三角形,若存在,求出a的值;若不存在,请说明理由.
(1)证明:xn+2-xn是常数,并求数列{xn}的通项公式;
(2)若l的方程为y=
| 1 |
| 4 |
| 1 |
| 12 |
分析:(1)根据△AnBnAn+1构成以Bn(n,yn)这顶点的等腰三角形,可得
=n,然后利用递推关系可得xn+2-xn是常数,最后讨论n的奇偶,可求出数列{xn}的通项公式;
(2)先分别求出|AnAn+1|与|BnCn|,要使△AnBnAn+1为直角三角形当且仅当|AnAn+1|=2|BnCn|,然后建立方程解之即可.
| xn+xn+1 |
| 2 |
(2)先分别求出|AnAn+1|与|BnCn|,要使△AnBnAn+1为直角三角形当且仅当|AnAn+1|=2|BnCn|,然后建立方程解之即可.
解答:解:(1)因△AnBnAn+1构成以Bn(n,yn)这顶点的等腰三角形,
∴
=n即xn+xn+1=2n(n∈N+)(1)
从而xn+1+xn+2=2(n+1)(2)
由(2)-(1)得,xn+2-xn=2,为常数.
显然x1,x3,x5,…x2n-1,…及x2,x4,x6,…x2n,…分别成等差数列.
∴x2n-1=x1+(n-1)×2=(2n-1)+a-1,x2n=x2+2(n-1)=(2-a)+2n-2,(n∈N+)
∴xn=
(2)当n为奇数时,An(n+a-1,0),An+1(n+1-a,0),∴|AnAn+1|=2(1-a)
当n为偶数时,An(n-a,0),An+1(n+a,0),∴|AnAn+1|=2a.
作BnCn⊥x轴于Cn,由于点Bn(n,yn)在直线l上,
∴yn=
n+
即|BnCn|=
n+
.
要使△AnBnAn+1为直角三角形当且仅当|AnAn+1|=2|BnCn|,
∴当n为奇数时,有2(1-a)=2(
n+
),即12a=11-3n,(※)
当n=1时,a=
,当n=3时,a=
,当n≥5时,方程(※)无解.
当n为偶数时,有12a=3n+1,同时可得a=
.
综上所述,当a=
或a=
或a=
,存在直角三角形.
∴
| xn+xn+1 |
| 2 |
从而xn+1+xn+2=2(n+1)(2)
由(2)-(1)得,xn+2-xn=2,为常数.
显然x1,x3,x5,…x2n-1,…及x2,x4,x6,…x2n,…分别成等差数列.
∴x2n-1=x1+(n-1)×2=(2n-1)+a-1,x2n=x2+2(n-1)=(2-a)+2n-2,(n∈N+)
∴xn=
|
(2)当n为奇数时,An(n+a-1,0),An+1(n+1-a,0),∴|AnAn+1|=2(1-a)
当n为偶数时,An(n-a,0),An+1(n+a,0),∴|AnAn+1|=2a.
作BnCn⊥x轴于Cn,由于点Bn(n,yn)在直线l上,
∴yn=
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
| 1 |
| 12 |
要使△AnBnAn+1为直角三角形当且仅当|AnAn+1|=2|BnCn|,
∴当n为奇数时,有2(1-a)=2(
| 1 |
| 4 |
| 1 |
| 12 |
当n=1时,a=
| 2 |
| 3 |
| 1 |
| 6 |
当n为偶数时,有12a=3n+1,同时可得a=
| 7 |
| 12 |
综上所述,当a=
| 2 |
| 3 |
| 1 |
| 6 |
| 7 |
| 12 |
点评:本题主要考查了等差数列的通项公式,以及直角三角形的判定,同时考查了分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数y=
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数y= 已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数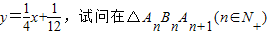 中是否存在直角三角形,若存在,求出a的值;若不存在,请说明理由.
中是否存在直角三角形,若存在,求出a的值;若不存在,请说明理由.