题目内容
已知周期函数f(x)的定义域为R,周期为2,且当-1<x≤1时,f(x)=1-x2.若直线y=-x+a与曲线y=f(x)恰有2个交点,则实数a的所有可能取值构成的集合为
- A.
 或
或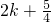 ,k∈Z}
,k∈Z} - B.
 或
或 ,k∈Z}
,k∈Z} - C.{a|a=2k+1或
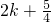 ,k∈Z}
,k∈Z} - D.{a|a=2k+1,k∈Z}
C
分析:由题意画出函数f(x)的图象,并在图中画出关键直线,再由条件转化为求出相切时的切点坐标,利用导数的几何意义,然后再把坐标代入切线方程求出a的值,
解答: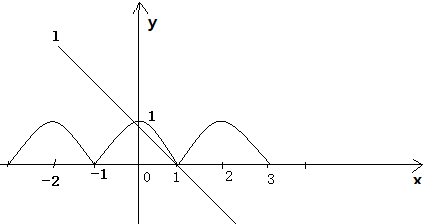 解:由题意画出函数f(x)的图象,如下图:
解:由题意画出函数f(x)的图象,如下图:
其中图中的直线l的方程为:y=-x+1,此时恰有两个交点,
由图得,当-1<x≤1时,直线l向上平移过程中与曲线y=f(x)恰有3个交点,
直到相切时,
设切点为p(x,y),则f′(x)=-2x,
∴-1=-2x,解得x= ,即y=f(
,即y=f( )=
)=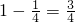 ,
,
∴p( ,
, ),代入切线y=-x+a,解得a=
),代入切线y=-x+a,解得a= ,
,
∵f(x)的定义域为R,周期为2,
∴所求的a的集合是:{a|a=2k+1或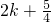 ,k∈Z},
,k∈Z},
故选C.
点评:本题考查了函数的性质以及图象的应用,导数的几何意义,考查了数形结合思想,关键正确作图.
分析:由题意画出函数f(x)的图象,并在图中画出关键直线,再由条件转化为求出相切时的切点坐标,利用导数的几何意义,然后再把坐标代入切线方程求出a的值,
解答:
 解:由题意画出函数f(x)的图象,如下图:
解:由题意画出函数f(x)的图象,如下图:其中图中的直线l的方程为:y=-x+1,此时恰有两个交点,
由图得,当-1<x≤1时,直线l向上平移过程中与曲线y=f(x)恰有3个交点,
直到相切时,
设切点为p(x,y),则f′(x)=-2x,
∴-1=-2x,解得x=
 ,即y=f(
,即y=f( )=
)=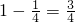 ,
,∴p(
 ,
, ),代入切线y=-x+a,解得a=
),代入切线y=-x+a,解得a= ,
,∵f(x)的定义域为R,周期为2,
∴所求的a的集合是:{a|a=2k+1或
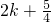 ,k∈Z},
,k∈Z},故选C.
点评:本题考查了函数的性质以及图象的应用,导数的几何意义,考查了数形结合思想,关键正确作图.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目