题目内容
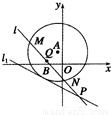
如图所示，已知以点A（-1，2）为圆心的圆与直线l1：x+2y+7=0相切．过点B（-2，0）的动直线l与圆A相交于M，N两点，Q是MN的中点，直线l与l1相交于点P．（1）求圆A的方程；
（2）当
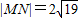时，求直线l的方程．
【答案】分析：（1）利用圆心到直线的距离公式求圆的半径，从而求解圆的方程；
（2）根据相交弦长公式，求出圆心到直线的距离，设出直线方程，再根据点到直线的距离公式确定直线方程．
解答：解：（1）设圆的半径R，则R=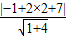
=2
，
∴圆的方程是（x+1）2+（y-2）2=20；
（2）设直线l的方程是x=my-2或y=0，
∵d圆心到直线=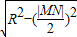
=1
∴
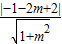=1⇒3m2-4m=0⇒m=0或
，y=0不成立，
∴直线l的方程是：x=-2或3x-4y+6=0
点评：本题考查圆的标准方程及直线与圆的相交弦长问题．弦长|MN|=2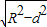
．
（2）根据相交弦长公式，求出圆心到直线的距离，设出直线方程，再根据点到直线的距离公式确定直线方程．
解答：解：（1）设圆的半径R，则R=
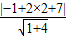=2，∴圆的方程是（x+1）2+（y-2）2=20；
（2）设直线l的方程是x=my-2或y=0，
∵d圆心到直线=
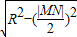=1∴
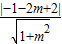=1⇒3m2-4m=0⇒m=0或，y=0不成立，∴直线l的方程是：x=-2或3x-4y+6=0
点评：本题考查圆的标准方程及直线与圆的相交弦长问题．弦长|MN|=2
． 
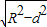练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
如图所示，已知以点A（-1，2）为圆心的圆与直线l1：x+2y+7=0相切．过点B（-2，0）的动直线l与圆A相交于M，N两点，Q是MN的中点，直线l与l1相交于点P．
一次机器人足球比赛中，甲队1号机器人由点A开始作匀速直线运动，到达点B时，发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动．如图所示，已知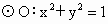
和定点A(2，1)，由⊙O外一点P(a，b)向⊙O引切线PQ，切点为Q，且满足|PQ|=|PA|．
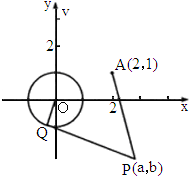
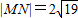时，求直线l的方程．