题目内容
(
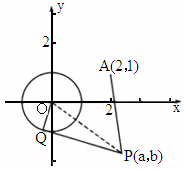
山东实验中学模拟)如图所示,已知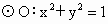 和定点A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
和定点A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
(1)
求实数a,b间满足的等量关系;(2)
求线段PQ长的最小值;(3)
若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程.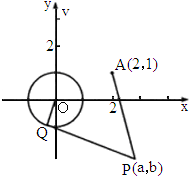
答案:略
解析:
解析:
|
解析: (1)连结OP,∵Q为切点,PQ⊥OQ,由勾股定理有
又由已知 |PQ|=|PA|,故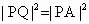 , ,
即 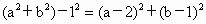 , ,
化简得实数 a、b间满足的等量关系为:2a +b-3=0.(2) 由2a+b-3=0,得b=-2a+3.
故当 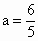 时, 时,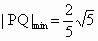 ,即线段PQ长的最小值为 ,即线段PQ长的最小值为 . .
(3) 设⊙P的半径为R,∵⊙ P与⊙O有公共点,⊙O的半径为1,∴ 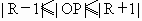 ,即 ,即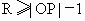 且 且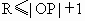 . .
而 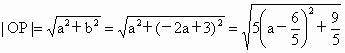 . .
故当 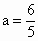 时, 时,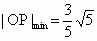 , ,
此时 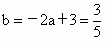 , ,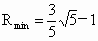 . .
得半径取最小值时⊙ P的方程为 . .
本题其它解法参照以上标准酌情给分. |

练习册系列答案
相关题目
(
山东实验中学模拟)已知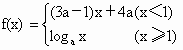 是R上的减函数,那么a的取值范围是
是R上的减函数,那么a的取值范围是
[
]|
A .(0,1) |
B .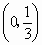 |
C .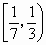 |
D .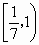 |
(
山东实验中学模拟)函数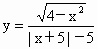 是
是
[
]|
A .奇函数不是偶函数 |
B .偶函数不是奇函数 |
|
C .既是奇函数又是偶函数 |
D .非奇非偶函数 |
(
山东实验中学模拟)已知两点M(-2,0),N(2,0),点P满足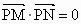 ,则点P的轨迹方程为
,则点P的轨迹方程为
[
]|
A .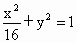 |
B .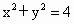 |
|
C .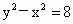 |
D .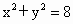 |
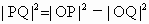
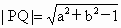
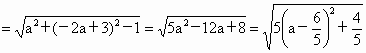
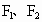 是双曲线
是双曲线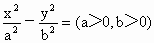 的两个焦点;P在双曲线上,若
的两个焦点;P在双曲线上,若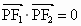 ,
,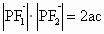 (c为半焦距),则双曲线的离心率为
(c为半焦距),则双曲线的离心率为
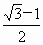
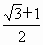
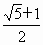
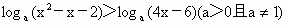 成立,则此不等式的解是_________.
成立,则此不等式的解是_________.