题目内容
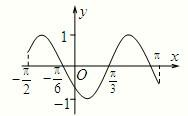函数y=f（x）在区间[-| π |
| 2 |
A、f(x)=sin(2x+
| ||
B、f(x)=sin(2x-
| ||
C、f(x)=sin(x+
| ||
D、f(x)=sin(x-
|
分析：根据图象的最高点和最低点，得到A的值，根据半个周期的长度得到ω的值，写出解析式，根据函数的图象过（
，0）点，代入点的坐标，求出φ的值，写出解析式．
| π |
| 3 |
解答：解：由图象知A=1，
∵
=
- (-
)=
，
∴T=π，
∴ω=2，
∴函数的解析式是y=sin（2x+φ）
∵函数的图象过（
，0）
∴0=sin（2×
+φ）
∴φ=kπ-
，
∴φ=
∴函数的解析式是y=sin（2x-
）
故选B．
∵
| T |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
∴T=π，
∴ω=2，
∴函数的解析式是y=sin（2x+φ）
∵函数的图象过（
| π |
| 3 |
∴0=sin（2×
| π |
| 3 |
∴φ=kπ-
| 2π |
| 3 |
∴φ=
| 2π |
| 3 |
∴函数的解析式是y=sin（2x-
| 2π |
| 3 |
故选B．
点评：本题考查由函数的图象求函数的解析式，本题解题的难点是求出解析式的初相，这里可以利用代入特殊点或五点对应法，本题是一个基础题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
（2011•花都区模拟）已知函数y=f（x）在定义域[-4，6]内可导，其图象如图，记y=f（x）的导函数为y=f′（x），则不等式f′（x）≥0的解集为（ ）
（2011•花都区模拟）已知函数y-f（x）在定义域[-4，6]内可导，其导函数y=f′（x）的图象如图，则函数y=f（x）的单调递增区间为（ ）