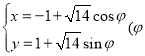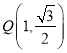题目内容
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且过点A(2,1).
,且过点A(2,1).
(1)求C的方程:
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)由题意得到关于a,b,c的方程组,求解方程组即可确定椭圆方程.
(2)设出点M,N的坐标,在斜率存在时设方程为![]() , 联立直线方程与椭圆方程,根据已知条件,已得到m,k的关系,进而得直线MN恒过定点,在直线斜率不存在时要单独验证,然后结合直角三角形的性质即可确定满足题意的点Q的位置.
, 联立直线方程与椭圆方程,根据已知条件,已得到m,k的关系,进而得直线MN恒过定点,在直线斜率不存在时要单独验证,然后结合直角三角形的性质即可确定满足题意的点Q的位置.
(1)由题意可得: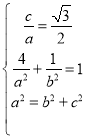 ,解得:
,解得:![]() ,故椭圆方程为:
,故椭圆方程为:![]() .
.
(2)设点![]() .
.
因为AM⊥AN,∴![]() ,即
,即![]() ,①
,①
当直线MN的斜率存在时,设方程为![]() ,如图1.
,如图1.
代入椭圆方程消去![]() 并整理得:
并整理得:![]() ,
,
![]() ②,
②,
根据![]() ,代入①整理可得:
,代入①整理可得:
![]()
将②代入,![]() ,
,
整理化简得![]() ,
,
∵![]() 不在直线
不在直线![]() 上,∴
上,∴![]() ,
,
∴![]() ,
,
于是MN的方程为![]() ,
,
所以直线过定点直线过定点![]() .
.
当直线MN的斜率不存在时,可得![]() ,如图2.
,如图2.
代入![]() 得
得![]() ,
,
结合![]() ,解得
,解得![]() ,
,
此时直线MN过点![]() ,
,
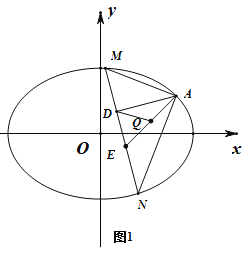
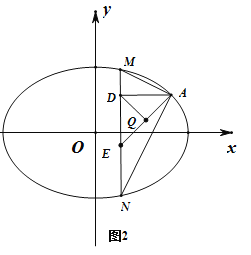
由于AE为定值,且△ADE为直角三角形,AE为斜边,
所以AE中点Q满足![]() 为定值(AE长度的一半
为定值(AE长度的一半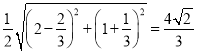 ).
).
由于![]() ,故由中点坐标公式可得
,故由中点坐标公式可得![]() .
.
故存在点![]() ,使得|DQ|为定值.
,使得|DQ|为定值.

【题目】将某公司200天的日销售收入(单位:万元)统计如下表(1)所示,
日销售收入 |
|
|
|
|
|
|
频数 | 12 | 28 | 36 | 54 | 50 | 20 |
频率 |
表(1)
(1)完成上述频率分布表,并估计公司这200天的日均销售收入(同一组中的数据用该组所在区间的中点值代表);
(2)已知该公司2020年第一、二季度的日销售收入如下表(2)所示,第三季度的日销售收入及其频率可用表(1)中的数据近似代替,且在2020年,当公司日销售收入为![]() 时,员工的日绩效为100元,当公司日销售收入为
时,员工的日绩效为100元,当公司日销售收入为![]() 时,员工的日绩效为200元,当公司日销售收入为
时,员工的日绩效为200元,当公司日销售收入为![]() 时,员工的日绩效为300元.以频率估计概率.
时,员工的日绩效为300元.以频率估计概率.
①若在第三季度某员工的工作日中随机抽取2天,记该员工2天的绩效之和为![]() ,求
,求![]() 的分布列以及数学期望;
的分布列以及数学期望;
②若每个员工每个季度的工作日为50天,估计2020年前三个季度每个员工获得的绩效的总额.
日销售收入 |
|
|
|
|
|
|
频率 | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 | 0.1 |
表(2)