题目内容
已知数列 为等差数列,若
为等差数列,若 ,且它们的前
,且它们的前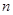 项和
项和 有最大值,则使
有最大值,则使 的
的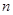 的最大值为( )
的最大值为( )
| A.19 | B.11 | C.20 | D.21 |
A
解析试题分析:由 ,得
,得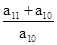 <0,由它们的前n项和Sn有最大值可得数列的公差d<0,
<0,由它们的前n项和Sn有最大值可得数列的公差d<0,
∴a10>0,a11+a10<0,a11<0,
∴a1+a19=2a10>0,a1+a20=a11+a10<0.使得Sn>0的n的最大值n=19,
故选A。
考点:本题主要考查等差数列的求和公式,等差数列的性质。
点评:中档题,本题较为典型,将等差数列的求和公式、等差数列的性质综合考查。确定公差d<0是具体地关键之一。

练习册系列答案
相关题目
数列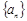 中,如果
中,如果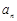 =
=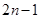 (n=1,2,3,…) ,那么这个数列是( ).
(n=1,2,3,…) ,那么这个数列是( ).
| A.公差为2的等差数列 | B.公差为-2的等差数列 |
| C.首项为-3的等差数列 | D.首项为-3的等比数列 |
设等差数列 的前
的前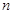 项和是
项和是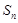 ,若
,若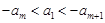 (
( N*,且
N*,且 ),则必定有( )
),则必定有( )
A. ,且 ,且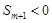 | B.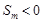 ,且 ,且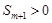 |
C. ,且 ,且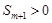 | D.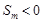 ,且 ,且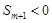 |
已知等差数列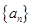 的公差和等比数列
的公差和等比数列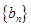 的公比都是
的公比都是 ,且
,且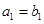 ,
,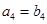 ,
,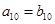 ,则
,则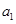 和
和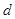 的值分别为( )
的值分别为( )
A.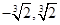 | B.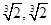 |
C.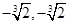 | D.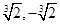 |
设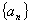 为等差数列,公差
为等差数列,公差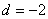 ,
,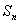 为其前
为其前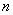 项和,若
项和,若 ,则
,则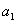 =
=
A. | B. |
C. | D.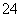 |
等差数列{an}的通项公式为an=2n+1,其前n项的和为Sn,则数列 的前10项的和为( ).
的前10项的和为( ).
| A.120 | B.70 | C.75 | D.100 |
在等差数列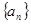 中
中 ,
, ,且
,且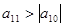 ,则在
,则在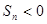 中,
中, 的最大值为( )
的最大值为( )
| A.17 | B.18 | C.19 | D.20 |
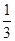 ,则D(3ξ-1)=( )
,则D(3ξ-1)=( )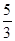 C、
C、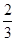 D、5
D、5  有两个不同的零点
有两个不同的零点 ,且方程
,且方程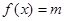 有两个不同的实根
有两个不同的实根 .若把这四个数按从小到大排列构成等差数列,则实数
.若把这四个数按从小到大排列构成等差数列,则实数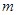 的值为
的值为