题目内容
已知函数 有两个不同的零点
有两个不同的零点 ,且方程
,且方程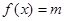 有两个不同的实根
有两个不同的实根 .若把这四个数按从小到大排列构成等差数列,则实数
.若把这四个数按从小到大排列构成等差数列,则实数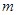 的值为
的值为
A.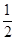 | B. | C.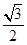 | D. |
D
解析试题分析:根据题意可知,由于函数 有两个不同的零点
有两个不同的零点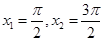 ,而对于方程
,而对于方程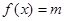 有两个不同的实根
有两个不同的实根 ,那么可知,两个根x3、x4只能分布在x1、x2的中间或两侧,若x3、x4只能分布在x1、x2的中间,则公差d=
,那么可知,两个根x3、x4只能分布在x1、x2的中间或两侧,若x3、x4只能分布在x1、x2的中间,则公差d=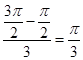
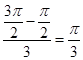 ,故x3、x4分别为
,故x3、x4分别为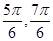 ,此时可求得m=cos
,此时可求得m=cos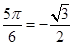
若x3、x4只能分布在x1、x2的两侧,则公差d=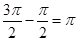
故x3、x4分别为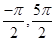 ,故可知不合题意,选D
,故可知不合题意,选D
考点:等差数列
点评:本题为等差数列的构成问题,涉及分类讨论的思想和函数的零点以及三角函数,属中档题.

练习册系列答案
相关题目
已知等差数列 的公差为2,若
的公差为2,若 成等比数列,则
成等比数列,则 =( )
=( )
A. | B. | C. | D. |
已知数列 的前
的前 项和为
项和为 ,
, =
= ,则
,则 ( )
( )
| A.6 | B.7 | C.8 | D.9 |
已知数列 为等差数列,若
为等差数列,若 ,且它们的前
,且它们的前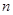 项和
项和 有最大值,则使
有最大值,则使 的
的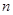 的最大值为( )
的最大值为( )
| A.19 | B.11 | C.20 | D.21 |
已知数列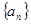 中, a2=7,且an =an+1-6(n∈
中, a2=7,且an =an+1-6(n∈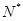 ),则前n项和Sn=" (" )
),则前n项和Sn=" (" )
A.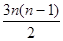 | B. n2 | C.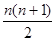 | D.3n2 –2n |
设等差数列 的前
的前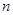 项和为
项和为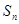 ,已知
,已知 ,
,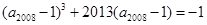 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.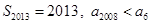 | B.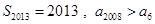 |
C.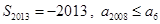 | D.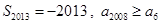 |
在等差数列 中每一项均不为0,若
中每一项均不为0,若 ,则
,则 ( )
( )
| A.2011 | B.2012 | C.2013 | D.2014 |
在等差数列 中,
中, +
+ =10则
=10则 的值为
的值为
| A.5 | B.6 | C.8 | D. 10 |
设 是公差不为0的等差数列
是公差不为0的等差数列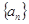 的前n项和,且
的前n项和,且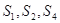 成等比数列,则
成等比数列,则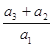 等于( )
等于( )
A.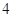 | B.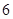 | C.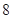 | D.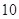 |