题目内容
等差数列{an}的通项公式为an=2n+1,其前n项的和为Sn,则数列 的前10项的和为( ).
的前10项的和为( ).
| A.120 | B.70 | C.75 | D.100 |
C
解析试题分析:因为,等差数列{an}的通项公式为an=2n+1,所以,其前n项的和Sn=n(n+2), ,
, 的前10项的和为75,故选C。
的前10项的和为75,故选C。
考点:本题主要考查倒靫收莲的通项公式、求和公式。
点评:简单题,注意分析发现 实际上是等差数列。
实际上是等差数列。

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
已知等差数列 的前13项和
的前13项和 ,则
,则 =( )
=( )
| A.3 | B.6 | C.9 | D.12 |
已知数列 为等差数列,若
为等差数列,若 ,且它们的前
,且它们的前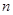 项和
项和 有最大值,则使
有最大值,则使 的
的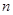 的最大值为( )
的最大值为( )
| A.19 | B.11 | C.20 | D.21 |
设等差数列 的前
的前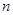 项和为
项和为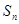 ,已知
,已知 ,
,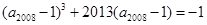 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.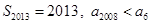 | B.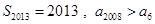 |
C.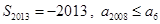 | D.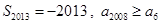 |
在等差数列 中每一项均不为0,若
中每一项均不为0,若 ,则
,则 ( )
( )
| A.2011 | B.2012 | C.2013 | D.2014 |
在等差数列 中,
中, +
+ =10则
=10则 的值为
的值为
| A.5 | B.6 | C.8 | D. 10 |
公差不为零的等差数列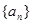 中,
中, ,数列
,数列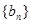 是等比数列,且
是等比数列,且  ( )
( )
| A.2 | B.4 | C.8 | D.16 |
已知等差数列{ }中,
}中,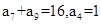 ,则
,则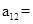 ( )
( )
| A.15 | B.30 | C.31 | D.64 |
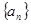 的前n项和为
的前n项和为 ,下列选项不可能是
,下列选项不可能是 的图像的是
的图像的是