题目内容
(14分)(2011•广东)在平面直角坐标系xOy中,直线l:x=﹣2交x轴于点A,设P是l上一点,M是线段OP的垂直平分线上一点,且满足∠MPO=∠AOP.
(1)当点P在l上运动时,求点M的轨迹E的方程;
(2)已知T(1,﹣1),设H是E上动点,求|HO|+|HT|的最小值,并给出此时点H的坐标;
(3)过点T(1,﹣1)且不平行与y轴的直线l1与轨迹E有且只有两个不同的交点,求直线l1的斜率k的取值范围.
(1)y2=4x+4 (x≥﹣1)或y=0(x<﹣1)
(2)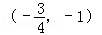
(3)(﹣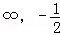 ]∪(0,+∞)
]∪(0,+∞)
解析试题分析:(1)由于直线l:x=﹣2交x轴于点A,所以A(﹣2,0),由于P是l上一点,M是线段OP的垂直平分线上一点,且满足∠MPO=∠AOP,可以设点P,由于满足∠MPO=∠AOP,所以分析出MN∥AO,利用相关点法可以求出动点M的轨迹方程;
(2)由题意及点M的轨迹E的方程为y2=4(x+1),且已知T(1,﹣1),又H是E 上动点,点O及点T都为定点,利用图形即可求出;
(3)由题意设出过定点的直线方程l1并与点M的轨迹E的方程联立,利用有两个交点等价与联立之后的一元二次方程的判别式大于0,即可得到所求.
解:(1)如图所示,连接OM,则|PM|=|OM|∵∠MPO=∠AOP,∴动点M满足MP⊥l或M在x的负半轴上,设M(x,y) ①当MP⊥l时,|MP|=|x+2|,|om|=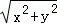 ,|x+2|=
,|x+2|=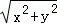 ,化简得y2=4x+4 (x≥﹣1)②当M在x的负半轴上时,y=0(x<﹣1)综上所述,点M的轨迹E的方程为y2=4x+4 (x≥﹣1)或y=0(x<﹣1)
,化简得y2=4x+4 (x≥﹣1)②当M在x的负半轴上时,y=0(x<﹣1)综上所述,点M的轨迹E的方程为y2=4x+4 (x≥﹣1)或y=0(x<﹣1)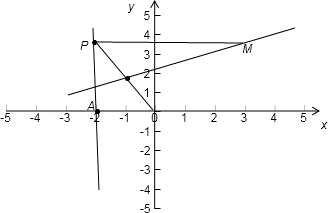
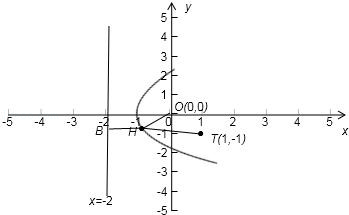
(2)由题意画出图形如下:
∵由(1)知道动点M 的轨迹方程为:y2=4(x+1).
是以(﹣1,0)为顶点,以O(0,0)为焦点,以x=﹣2为准线的抛物线,
由H引直线HB垂直准线x=﹣2与B点,则
利用抛物线的定义可以得到:|HB|=|HO|,
∴要求|HO|+|HT|的最小值等价于求折线|HB|+|HT|的最小值,
由图可知当由点T直接向准线引垂线是与抛物线相交的H使得HB|+|HT|的最小值,
故|HO|+|HT|的最小值时的H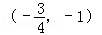 .
.
(3)如图,设抛物线顶点A(﹣1,0),则直线AT的斜率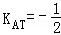 ∵点T(1,﹣1)在抛物线内部,∴过点T且不平行于x,y轴的直线l1必与抛物线有两个交点则直线l1与轨迹E的交点个数分以下四种情况讨论:①当K
∵点T(1,﹣1)在抛物线内部,∴过点T且不平行于x,y轴的直线l1必与抛物线有两个交点则直线l1与轨迹E的交点个数分以下四种情况讨论:①当K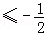 时,直线l1与轨迹E有且只有两个不同的交点 ②当
时,直线l1与轨迹E有且只有两个不同的交点 ②当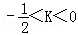 时,直线l1与轨迹E有且只有三个不同的交点 ③当K=0时,直线l1与轨迹E有且只有一个交点 ④当K>0时,直线l1与轨迹E有且只有两个不同的交点综上所述,直线l1的斜率K的取值范围是
时,直线l1与轨迹E有且只有三个不同的交点 ③当K=0时,直线l1与轨迹E有且只有一个交点 ④当K>0时,直线l1与轨迹E有且只有两个不同的交点综上所述,直线l1的斜率K的取值范围是
(﹣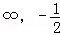 ]∪(0,+∞)
]∪(0,+∞) 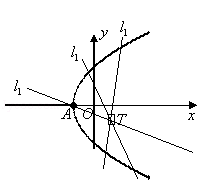
点评:此题重点考查了利用相关点法求动点的轨迹方程,还考查了利用抛物线的定义求出HO|+|HT|的最小值时等价转化的思想,还考查了直线与曲线有两个交点的等价转化思想.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案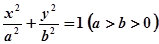 的离心率
的离心率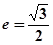 ,
,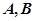 分别为椭圆的长轴和短轴的端点,
分别为椭圆的长轴和短轴的端点,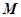 为
为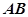 中点,
中点,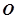 为坐标原点,且
为坐标原点,且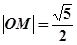 .
.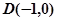 的直线
的直线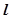 交椭圆于
交椭圆于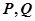 两点,求
两点,求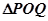 面积最大时,直线
面积最大时,直线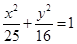 的右焦点为
的右焦点为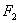 ,点
,点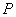 是椭圆上任意一点,圆
是椭圆上任意一点,圆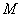 是以
是以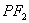 为直径的圆.
为直径的圆. ,求圆
,求圆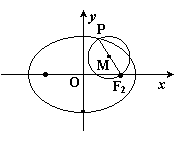
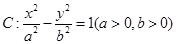 的两个焦点为
的两个焦点为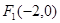 、
、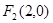 点
点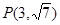 在双曲线C上.
在双曲线C上.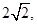 求直线l的方程.
求直线l的方程.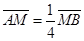 ,求直线l的方程;
,求直线l的方程;
 中,已知椭圆
中,已知椭圆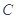 ∶
∶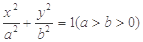 的左、右焦点分别
的左、右焦点分别 、
、 焦距为
焦距为 ,且与双曲线
,且与双曲线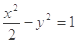 共顶点.
共顶点.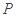 为椭圆
为椭圆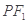 交椭圆
交椭圆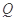 .
.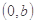 ,求过
,求过
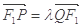 ,且
,且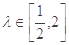 ,求
,求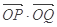 的最大值.
的最大值.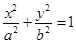 的一个焦点为
的一个焦点为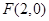 ,且离心率为
,且离心率为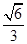 .
.  的直线
的直线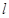 过点
过点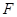 ,且与椭圆交于
,且与椭圆交于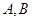 两点,
两点,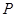 为直线
为直线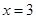 上的一点,若△
上的一点,若△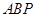 为等边三角形,求直线
为等边三角形,求直线 面积的最小值.
面积的最小值.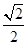 .
.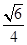 .若A、B两点关于x轴对称,E为线段AB的中点,射线OE交椭圆C于点P.如果
.若A、B两点关于x轴对称,E为线段AB的中点,射线OE交椭圆C于点P.如果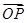 =t
=t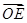 ,求实数t的值.
,求实数t的值.