题目内容
（本小题满分12分）
已知椭圆
（常数
、
，且
）的左右焦点分别为
，M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形．
(Ⅰ)求椭圆方程；
(Ⅱ)过原点且斜率分别为k和－k（k≥2）的两条直线与椭圆
的交点为A、B、C、D（按逆时针顺序排列，且点A位于第一象限内），求四边形ABCD的面积S的最大值．.
解: (Ⅰ)依题意: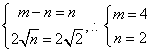
,
所求椭圆方程为
.………………………3分
(Ⅱ)设A(x,y).由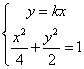
得
.………………………6分
根据题设直线图象与椭圆的对称性,知…………8分
…………9分∴
设
则
当
时，
∴
在
时单调递增，∴
………11分
∴当时，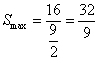
.………………………12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
