Question

已知圆C过定点A(0，p)(p＞0)，圆心C在抛物线x²=2py上运动，若MN为圆C在x轴上截得的弦，设｜AM｜=m,｜AN｜=n，∠MAN=θ.

(1)当点C运动时，｜MN｜是否变化?写出并证明你的结论?

(2)求+的最大值，并求取得最大值时θ的值和此时圆C的方程.若不存在，说明理由

Answer 1

(1)｜MN｜=2p不变化  

（2）2 ， θ=45°圆的方程为(x- p)²+(y-p)²=2p²或(x+p)²+(y-p)²=2p²

解析:

(1)设圆心C(x₀,y₀),则x²₀=2py₀，圆C的半径｜CA｜=，其方程为(x-x₀)²+(y-y₀)²=x²₀+(y₀-p)²,令y=0，并将x²₀=2py₀，代入，得x²-2x₀x+x²₀-p²=0，解得x_m=x₀-p,x_N=x₀+p,∴｜MN｜=｜x_N-x_M｜=2p(定值)

(2)∵m=｜AM｜=,n=｜AN｜=,∴m²+n²=4p²+2x²₀,m·n=，∴+====

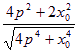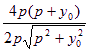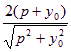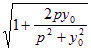=2≤2，当且仅当y₀=p时等号成立，x₀=±p，此时△MCN为等腰直角三角形，且∠MCN=90°，∴∠MAN=∠MCN=45°，故当θ=45°时，圆的方程为(x- p)²+(y-p)²=2p²或(x+p)²+(y-p)²=2p²