题目内容
某市有大型超市200家、中型超市400家、小型超市1400家,为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市( )
| A.70家 | B.50家 | C.20家 | D.10家 |
C
解析试题分析:∵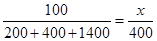 ,∴
,∴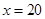 .
.
考点:分层抽样.

练习册系列答案
相关题目
某路段的雷达测速区检测点,对过往汽车的车速进行检测所得结果进行抽样分析,并绘制如图所示的时速(单位km/h)频率分布直方图,若在某一时间内有200辆汽车通过该检测点,请你根据直方图的数据估计在这200辆汽车中时速超过65km/h的约有( )
A.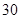 辆 辆 | B.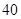 辆 辆 | C. 辆 辆 | D. 辆 辆 |
下表提供了某厂节能降耗技术改造后生产某产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨)的几组对应数据. 根据表中提供的数据,求出
(吨)的几组对应数据. 根据表中提供的数据,求出 关于
关于 的线性回归方程是
的线性回归方程是 ,那么表中
,那么表中 的值是( )
的值是( )
 | 3 | 4 | 5 | 6 |
 | 2.5 |  | 4 | 4.5 |
A.
 B.
B. C.
C. D.
D.
下表是某厂1—4月份用水量(单位:百吨)的一组数据:
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
由散点图可知,用水量与月份之间有较好的线性相关关系,其线性回归方程为
 =-0.7x+a,则a等于( )
=-0.7x+a,则a等于( )A.10.5 B.5.15 C.5.2 D.5.25
一个容量为20的样本,数据的分组及各组的频数如下:
(10,20 ,2;(20,30
,2;(20,30 ,3;(30,40
,3;(30,40 ,4;(40,50
,4;(40,50 ,5;(50,60
,5;(50,60 ,4;(60,70
,4;(60,70 ,2.
,2.
则样本在区间(10,50 上的频率为( )
上的频率为( )
| A.0.5 | B.0.7 | C.0.25 | D.0.05 |
在独立性检验中,统计量 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当
 3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的 ="20." 87,根据这一数据分析,认为打鼾与患心脏病之间
="20." 87,根据这一数据分析,认为打鼾与患心脏病之间
| A.有95%的把握认为两者有关 |
| B.约有95%的打鼾者患心脏病 |
| C.有99%的把握认为两者有关 |
| D.约有99%的打鼾者患心脏病 |
某产品的广告费用x与销售额y的统计数据如下表:
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 58 |
根据上表可得回归方程
 中的
中的 ,据此模型预报广告费用为
,据此模型预报广告费用为 万元时销售额为( ).
万元时销售额为( ).A.
 万元 B.
万元 B. 万元 C.
万元 C.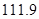 万元 D.
万元 D.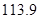 万元
万元 
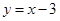


 设其平均数为
设其平均数为 ,中位数为
,中位数为 ,众数为
,众数为 ,则有( )
,则有( ) B.
B. C.
C. D.
D.