题目内容
在极坐标系中,圆ρ=4被直线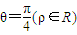 分成两部分的面积之比是 .
分成两部分的面积之比是 .
【答案】分析:利用圆ρ=4和直线θ=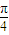 在极坐标系中特殊位置可知,圆是以极点为圆心,4为半径的圆,直线是过极点且倾斜角为
在极坐标系中特殊位置可知,圆是以极点为圆心,4为半径的圆,直线是过极点且倾斜角为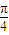 的直线,再利用圆的对称性质求解即可.
的直线,再利用圆的对称性质求解即可.
解答:解:∵直线θ=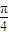 的过圆ρ=4的圆心,
的过圆ρ=4的圆心,
∴直线把圆分成两部分的面积之比是1:1.
故答案为1:1.
点评:本题主要考查了简单曲线的极坐标方程,圆的性质等,属于基础题.
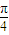 在极坐标系中特殊位置可知,圆是以极点为圆心,4为半径的圆,直线是过极点且倾斜角为
在极坐标系中特殊位置可知,圆是以极点为圆心,4为半径的圆,直线是过极点且倾斜角为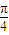 的直线,再利用圆的对称性质求解即可.
的直线,再利用圆的对称性质求解即可.解答:解:∵直线θ=
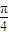 的过圆ρ=4的圆心,
的过圆ρ=4的圆心,∴直线把圆分成两部分的面积之比是1:1.
故答案为1:1.
点评:本题主要考查了简单曲线的极坐标方程,圆的性质等,属于基础题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目