题目内容
设l,m,n表示三条不同的直线,α,β,γ表示三个不同的平面,给出下列四个命题:
①若l⊥α,m⊥α,则l∥m;
②若m?α,m∥n,则n∥α;
③若m?β,n是l在β内的射影,m⊥l,则m⊥n;
④若α⊥γ,β⊥γ,则α∥β.
其中正确的命题是
①若l⊥α,m⊥α,则l∥m;
②若m?α,m∥n,则n∥α;
③若m?β,n是l在β内的射影,m⊥l,则m⊥n;
④若α⊥γ,β⊥γ,则α∥β.
其中正确的命题是
①③
①③
.分析:利用空间中直线与平面之间的位置关系及平面与平面之间的位置关系对①②③④诸选项一一判断即可.
解答:解:①∵l⊥α,m⊥α,
∴l∥m(垂直于同一平面的两直线平行),故①正确;
②m?α,m∥n,则n∥α或n?α,故②错误;
③∵m?β,n是l在β内的射影,m⊥l,
∴由三垂线定理的逆定理知,m⊥n,故③正确;
④α⊥γ,β⊥γ,如图:
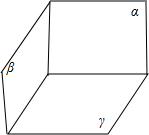
显然此时α与β相交,故④错误.
故答案为:①③.
∴l∥m(垂直于同一平面的两直线平行),故①正确;
②m?α,m∥n,则n∥α或n?α,故②错误;
③∵m?β,n是l在β内的射影,m⊥l,
∴由三垂线定理的逆定理知,m⊥n,故③正确;
④α⊥γ,β⊥γ,如图:

显然此时α与β相交,故④错误.
故答案为:①③.
点评:本题考查命题的真假判断与应用,着重考查空间中直线与平面之间的位置关系及平面与平面之间的位置关系,属于中档题.

练习册系列答案
相关题目