题目内容
已知函数y=(1)当x∈(0,+∞)时,函数的最大值;
(2)当x∈[2,+∞)时,函数的最大值.
思路点拨:求函数的最大值,可以根据函数的特点对函数解析式进行变形,本题由于分子是一次式,分母是二次式,所以可以变形为y=![]() 这种形式,然后根据均值定理和函数y=x+
这种形式,然后根据均值定理和函数y=x+![]() 的单调性求得最大值;另一方面我们也可以把函数解析式转化成方程,然后根据方程有根的情况求得y的最大值.
的单调性求得最大值;另一方面我们也可以把函数解析式转化成方程,然后根据方程有根的情况求得y的最大值.
解法一:把y=![]() 变形为y=
变形为y=![]() ,
,
(1)当x∈(0,+∞)时,由于x+![]() ≥2(当且仅当x=1时,取“=”),
≥2(当且仅当x=1时,取“=”),
∴y≤40(当且仅当x=1时,取“=”),即y的最大值是40.
(2)当x∈[2,+∞)时,x+![]() 是x的增函数,∴当x=2时,x+
是x的增函数,∴当x=2时,x+![]() 取得最小值
取得最小值![]() ,因此,当x=2时y=
,因此,当x=2时y=![]() 取得最大值32.
取得最大值32.
解法二:由y=![]() 变形得yx2-80x+y=0.
变形得yx2-80x+y=0.
(1)∵x∈(0,+∞),因此方程yx2-80x+y=0的判别式Δ=802-4y2≥0,
∴-40≤y≤40.当y=40时,代入方程yx2-80x+y=0可得x=1,适合x>0,
∴y的最大值为40.(当x=1时取得)
(2)∵x∈[2,+∞),
∴关于x的方程yx2-80x+y=0应该有不小于2的解,当且仅当方程yx2-80x+y=0的大根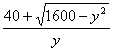 ≥2(其中y大于0),解得0<y≤32.
≥2(其中y大于0),解得0<y≤32.
∴y的最大值为32(当x=2时取得,即把y=32代入方程yx2-80x+y=0求得x=2).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
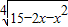 .求函数的单调区间和奇偶性.
.求函数的单调区间和奇偶性.