题目内容
(1)已知幂函数y=xm-2(x∈N)的图象与x,y轴都无交点,且关于y轴对称,求函数解析式.(2)已知函数y=
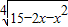 .求函数的单调区间和奇偶性.
.求函数的单调区间和奇偶性.
【答案】分析:(1)有幂函数的性质判断出幂函数的指数小于或等于0;指数为偶数.列出不等式求出m;
(2)根据函数奇偶性的定义,求出f(-x)的表达式并判断f(-x)与f(x)的关系,即可判断f(x)的奇偶性;函数为复合函数,据符号函数的单调性同增异减,外函数是减函数,求出内函数的递增区间为函数的递减区间;内函数的递减区间为函数的递增区间.
解答:解:(1)∵幂函数y=xm-2(m∈N)的图象与x轴,y轴都无交点,
∴m-2≤0,解得m≤2,又m∈N
∴m=0或m=1或m=2,又关于y轴对称,
∴m=0或m=2,
∴f(x)=x-2或f(x)=x=1(x≠0);
(2)由15-2x-x2≥0得函数的定义域为[-5,3],函数的定义域关于原点不对称,
∴函数既不是奇函数也不是偶函数.又对称轴为x=1,
∴x∈[-5,1]时,t随x的增大而增大;x∈(1,3)时,t随x的增大而减小.
又∵函数y=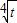 在t∈[0,16]时,y随t的增大而增大,
在t∈[0,16]时,y随t的增大而增大,
∴函数y=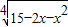 的单调增区间为[-5,1],单调减区间为(1,3).
的单调增区间为[-5,1],单调减区间为(1,3).
点评:本题考查幂函数的性质与幂指数的取值范围有关、考查二次函数的图象和性质,熟练掌握函数图象与性质的关系及判断方法是解答本题的关键.
(2)根据函数奇偶性的定义,求出f(-x)的表达式并判断f(-x)与f(x)的关系,即可判断f(x)的奇偶性;函数为复合函数,据符号函数的单调性同增异减,外函数是减函数,求出内函数的递增区间为函数的递减区间;内函数的递减区间为函数的递增区间.
解答:解:(1)∵幂函数y=xm-2(m∈N)的图象与x轴,y轴都无交点,
∴m-2≤0,解得m≤2,又m∈N
∴m=0或m=1或m=2,又关于y轴对称,
∴m=0或m=2,
∴f(x)=x-2或f(x)=x=1(x≠0);
(2)由15-2x-x2≥0得函数的定义域为[-5,3],函数的定义域关于原点不对称,
∴函数既不是奇函数也不是偶函数.又对称轴为x=1,
∴x∈[-5,1]时,t随x的增大而增大;x∈(1,3)时,t随x的增大而减小.
又∵函数y=
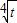 在t∈[0,16]时,y随t的增大而增大,
在t∈[0,16]时,y随t的增大而增大,∴函数y=
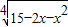 的单调增区间为[-5,1],单调减区间为(1,3).
的单调增区间为[-5,1],单调减区间为(1,3).点评:本题考查幂函数的性质与幂指数的取值范围有关、考查二次函数的图象和性质,熟练掌握函数图象与性质的关系及判断方法是解答本题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
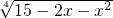 .求函数的单调区间和奇偶性.
.求函数的单调区间和奇偶性.