题目内容
设圆满足：①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长之比为3：1；③圆心到直线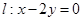
的距离为
，求该圆的方程．
【答案】
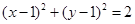或
【解析】
试题分析：求圆的方程关键就是要找到三个条件，求出相应的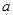
，
，
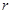.由①利用常用的半弦长、半径、弦心距三者构成的三角形可得
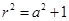，由②条件可得劣弧所对的圆心角为
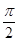，所以可得
，由③可得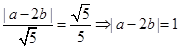
.通过解方程可求出，，.
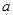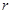试题解析：设圆心为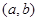
，半径为r，圆的方程为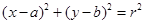
由条件①：，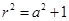
由条件②：，
从而有：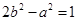
．由条件③：，
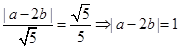解方程组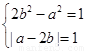
可得：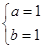
或
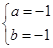，所以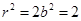
．
故所求圆的方程是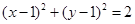或．
考点：1.圆中的重要三角形.2.点到直线的距离.3.弧长与圆心角的关系.
练习册系列答案
相关题目
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分，请在答题纸指定区域内作答，解答应写出文字说明、证明过程或演算步骤．
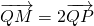的点M的轨迹为曲线C．
的点M的轨迹为曲线C．
的点M的轨迹为曲线C．