题目内容
【题目】已知椭圆E： 
（a＞b＞0）的左焦点F1与抛物线y2=﹣4x的焦点重合，椭圆E的离心率为 
，过点M（m，0）（m＞ 
）做斜率存在且不为0的直线l，交椭圆E于A，C两点，点P（ 
，0），且 
为定值．
（1）求椭圆E的方程；
（2）过点M且垂直于l的直线与椭圆E交于B，D两点，求四边形ABCD面积的最小值．
【答案】
（1）
解：抛物线y2=﹣4x的焦点为（﹣1，0），∴F1（1，0），∴c=1，又 
，a2=b2+c2，
解得c=1=b，a2=2．
∴椭圆E的方程为： 
+y2=1
（2）
解：设直线l的方程为：ty+m=x，A（x1，y1），C（x2，y2）．
联立 
，化为：（t2+2）y2+2tmy+m2﹣2=0．
△＞0，∴y1+y2= 
，y1y2= 
．
= 
+y1y2= 
+y1y2
= 
（y1+y2）+（t2+1）y1y2+ 
= +（t2+1） + = 
为定值．
∴ 
= 
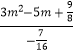，化为：3m2﹣5m+2=0， 
，解得m=1．
∴M（1，0）．
∴y1+y2= 
，y1y2= 
．
∴|AC|= 
= 
= 
，
把 
代换t可得：|BD|= 
．
∴S四边形ABCD= 
|AC||BD|= × × = 
，
令t2+1=k＞1，则f（k）= 
= 
= 
= 
≥ 
，
当 
= ，即k=2，t=±1时取等号．
∴四边形ABCD面积的最小值为
【解析】（1）抛物线y2=﹣4x的焦点为（﹣1，0），可得c=1，又 ，a2=b2+c2 ， 联立解出即可得出．（2）设直线l的方程为：ty+m=x，A（x1 ， y1），C（x2 ， y2）．与椭圆方程联立化为：（t2+2）y2+2tmy+m2﹣2=0．把根与系数的关系代入 = +y1y2= （y1+y2）+（t2+1）y1y2+ = 为定值．可得 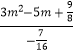= ，解得m=1．可得|AC|= = ，把 代换t可得：|BD|= ．利用S四边形ABCD= |AC||BD|与二次函数的单调性即可得出．
