题目内容
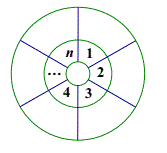
【题目】如图所示将同心圆环均匀分成n(
)格.在内环中固定数字1~n.问能否将数字1~n填入外环格内，使得外环旋转任意格后有且仅有一个格中内外环的数字相同？
【答案】见解析
【解析】
设对应于内环1，2，…，n的外环数字为i1，i2，…，in，它是数字1，2，…，n的一个排列.对k=1，2，…，n，记外环数字ik在按顺时针方向转动jk格时，和内环数字相同，即
,k=1，2，…，n.
根据题意，j1，j2，…，jn应是0，1，2，…，n-1的排列.求和
.
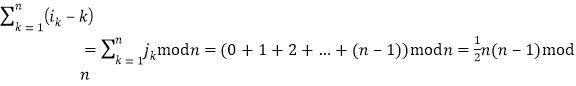于是n必须是奇数.
对于奇数n，我们取in=n，im=n-m，(m=1，2，…，n-1)，可以验证
jn=0, jn-1=2，jn-2=4，…，
，
j1=n-2, jn-1=n-4，j3=n-6，…，
，
符合题目要求.
练习册系列答案
名师点拨卷系列答案
相关题目
