题目内容
设a为实数,记函数 的最大值为g(a).
的最大值为g(a).(1)设t=
 ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);(2)求g(a).
【答案】分析:(1)令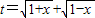 ,由1+x≥0且1-x≥0,得-1≤x≤1,再由
,由1+x≥0且1-x≥0,得-1≤x≤1,再由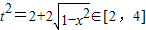 ,且t≥0…①,可得t的取值范围是
,且t≥0…①,可得t的取值范围是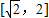 ,进而得m(t)的解析式.
,进而得m(t)的解析式.
(2)由题意知g(a)即为函数m(t)=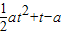 ,
,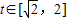 的最大值,直线
的最大值,直线 是抛物线m(t)=
是抛物线m(t)=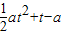 的对称轴,分a>0、a=0、a<0三种情况利用函数的单调性求出函数f(x)的最大值为g(a).
的对称轴,分a>0、a=0、a<0三种情况利用函数的单调性求出函数f(x)的最大值为g(a).
解答:解:(1)∵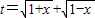 ,∴要使t有意义,必须1+x≥0且1-x≥0,即-1≤x≤1.
,∴要使t有意义,必须1+x≥0且1-x≥0,即-1≤x≤1.
∵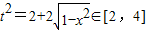 ,且t≥0…①,∴t的取值范围是
,且t≥0…①,∴t的取值范围是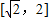 .
.
由①得: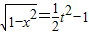 ,∴
,∴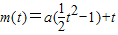 =
=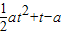 ,
,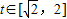 .
.
(2)由题意知g(a)即为函数m(t)=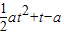 ,
,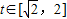 的最大值,
的最大值,
∵直线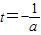 是抛物线m(t)=
是抛物线m(t)=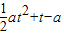 的对称轴,∴可分以下几种情况进行讨论:
的对称轴,∴可分以下几种情况进行讨论:
1)当a>0时,函数y=m(t),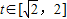 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由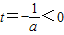 知m(t)在
知m(t)在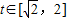 上单调递增,故g(a)=m(2)=a+2;
上单调递增,故g(a)=m(2)=a+2;
2)当a=0时,m(t)=t,在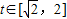 上单调递增,有g(a)=2;
上单调递增,有g(a)=2;
3)当a<0时,,函数y=m(t),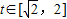 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若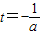
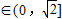 即
即 时,g(a)=
时,g(a)=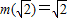 ,
,
若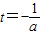
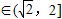 即
即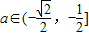 时,g(a)=
时,g(a)=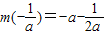 ,
,
若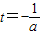 ∈(2,+∞)即
∈(2,+∞)即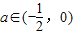 时,g(a)=m(2)=a+2.
时,g(a)=m(2)=a+2.
综上所述,有g(a)=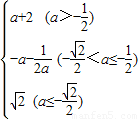 .
.
点评:本题主要考查二次函数在闭区间上的最值的求法,函数解析式求解的方法,体现了分类讨论的数学思想.
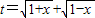 ,由1+x≥0且1-x≥0,得-1≤x≤1,再由
,由1+x≥0且1-x≥0,得-1≤x≤1,再由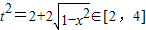 ,且t≥0…①,可得t的取值范围是
,且t≥0…①,可得t的取值范围是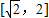 ,进而得m(t)的解析式.
,进而得m(t)的解析式.(2)由题意知g(a)即为函数m(t)=
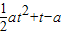 ,
,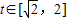 的最大值,直线
的最大值,直线 是抛物线m(t)=
是抛物线m(t)=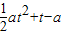 的对称轴,分a>0、a=0、a<0三种情况利用函数的单调性求出函数f(x)的最大值为g(a).
的对称轴,分a>0、a=0、a<0三种情况利用函数的单调性求出函数f(x)的最大值为g(a).解答:解:(1)∵
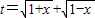 ,∴要使t有意义,必须1+x≥0且1-x≥0,即-1≤x≤1.
,∴要使t有意义,必须1+x≥0且1-x≥0,即-1≤x≤1.∵
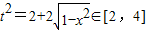 ,且t≥0…①,∴t的取值范围是
,且t≥0…①,∴t的取值范围是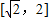 .
.由①得:
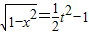 ,∴
,∴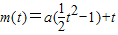 =
=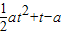 ,
,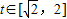 .
.(2)由题意知g(a)即为函数m(t)=
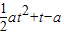 ,
,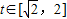 的最大值,
的最大值,∵直线
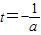 是抛物线m(t)=
是抛物线m(t)=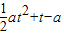 的对称轴,∴可分以下几种情况进行讨论:
的对称轴,∴可分以下几种情况进行讨论:1)当a>0时,函数y=m(t),
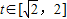 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,由
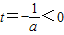 知m(t)在
知m(t)在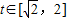 上单调递增,故g(a)=m(2)=a+2;
上单调递增,故g(a)=m(2)=a+2;2)当a=0时,m(t)=t,在
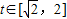 上单调递增,有g(a)=2;
上单调递增,有g(a)=2;3)当a<0时,,函数y=m(t),
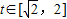 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,若
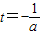
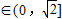 即
即 时,g(a)=
时,g(a)=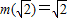 ,
,若
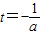
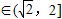 即
即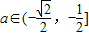 时,g(a)=
时,g(a)=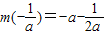 ,
,若
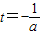 ∈(2,+∞)即
∈(2,+∞)即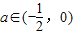 时,g(a)=m(2)=a+2.
时,g(a)=m(2)=a+2.综上所述,有g(a)=
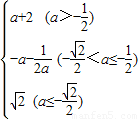 .
.点评:本题主要考查二次函数在闭区间上的最值的求法,函数解析式求解的方法,体现了分类讨论的数学思想.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
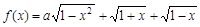 的最大值为
的最大值为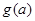 .
.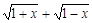 ,求t的取值范围,并把f(x)表示为t的函数m(t) ;
,求t的取值范围,并把f(x)表示为t的函数m(t) ;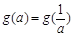 的所有实数a.
的所有实数a.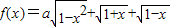 的最大值为g(a).
的最大值为g(a).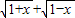 ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);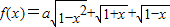 的最大值为g(a).
的最大值为g(a).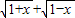 ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);