题目内容
已知:对于任意的多项式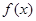 与任意复数z,
与任意复数z,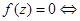
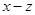 整除
整除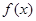 。利用上述定理解决下列问题:
。利用上述定理解决下列问题:
在复数范围内分解因式: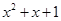 ;
;
求所有满足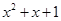 整除
整除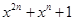 的正整数n构成的集合A。
的正整数n构成的集合A。
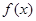 与任意复数z,
与任意复数z,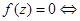
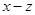 整除
整除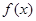 。利用上述定理解决下列问题:
。利用上述定理解决下列问题:在复数范围内分解因式:
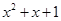 ;
;求所有满足
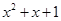 整除
整除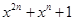 的正整数n构成的集合A。
的正整数n构成的集合A。(1)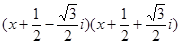 ;(2)
;(2) 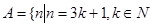 或
或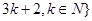 。
。
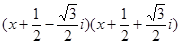 ;(2)
;(2) 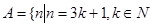 或
或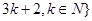 。
。 试题分析:(1) 令
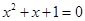 ,由求根公式可得两根为
,由求根公式可得两根为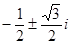 ;(2)因为
;(2)因为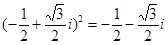 ,
,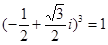 ,又一个整数除以
,又一个整数除以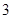 ,要么整除,要么余
,要么整除,要么余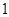 ,要么余
,要么余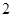 ,故分
,故分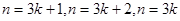 ,三种情况讨论。
,三种情况讨论。试题解析:(1)令
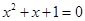 解得两个根
解得两个根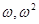 ,这里
,这里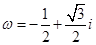
所以
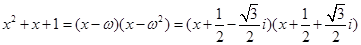
(2)记
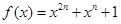 。
。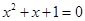 有两个根
有两个根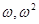 ,这里
,这里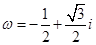 ,
,
当
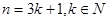 时,
时,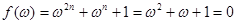 ,
,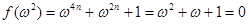 ,故在这种情形有
,故在这种情形有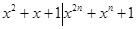 ,
,同样可以证明,当
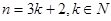 时,有
时,有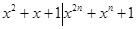 ,
,但当
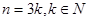 时,
时,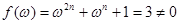 ,故
,故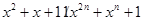 ,
,综上,当且仅当
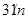 时,
时,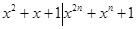 ,
,所以
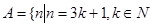 或
或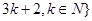 。
。 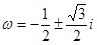 性质的应用。
性质的应用。 
练习册系列答案
相关题目
 ,
, .
. 为纯虚数,求实数
为纯虚数,求实数 的值;
的值;  ,请问复数
,请问复数 在复平面内对应的点在第几象限?
在复平面内对应的点在第几象限? = ( )
= ( )



 ( )
( ) 

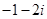

 =( )
=( ) ( )
( )  的值等于( )
的值等于( )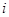 是虚数单位,复数
是虚数单位,复数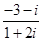 =( )
=( )


