Question

已知f（x）是二次函数，不等式f（x）＜0的解集是（0，5），且f（x）在区间[-1，4]上的最大值是12．
（1）求f（x）的解析式；
（2）是否存在实数m，使得方程f(x)+

37

x

=0在区间（m，m+1）内有且只有两个不等的实数根？若存在，求出m的取值范围；若不存在，说明理由．

Answer 1

分析：（1）根据二次函数小于0的解集，设出解析式，利用单调性求得最大值，解出待定系数．
（2）将方程等价转化h（x）=0，利用h（x）的导数判断其单调性，利用单调性判断h（x）=0的根的情况．

解答：解：（1）∵f（x）是二次函数，且f（x）＜0的解集是（0，5），∴可设f（x）=ax（x-5）（a＞0）．
∴f（x）在区间[-1，4]上的最大值是f（-1）=6a．
由已知得6a=12，∴a=2，∴f（x）=2x（x-5）=2x²-10x（x∈R）．
（2）方程f(x)+

37

x

=0等价于方程 2x³-10x²+37=0．
设h（x）=2x³-10x²+37，则h'（x）=6x²-20x=2x（3x-10）．
在区间x∈(0，

10

3

)时，h'（x）＜0，h（x）是减函数；
在区间（-∞，0），或(

10

3

，+∞)上，h'（x）＞0，h（x）是增函数，故h（0）是极大值，h（

10

3

）是极小值．
∵h(3)=1＞0，h(

10

3

)=-

1

27

＜0，h(4)=5＞0，
∴方程h（x）=0在区间(3，

10

3

)，(

10

3

，4)内分别有惟一实数根，故函数h（x）在（3，4）内有2个零点．
而在区间（0，3），（4，+∞）内没有零点，在（-∞，0）上有唯一的零点．
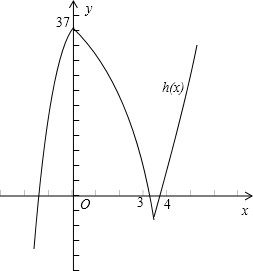
画出函数h（x）的单调性和零点情况的简图，如图所示．
所以存在惟一的自然数m=3，使得方程f(x)+

37

x

=0在区间（m，m+1）内有且只有两个不同的实数根．

点评：本小题主要考查函数的单调性、极值等基本知识，考查运用导数研究函数的性质的方法，考查函数与方程、数形结合等数学思想方法和分析问题、解决问题的能力．