题目内容
（14分）已知函数
在
处取得极值.
（Ⅰ）求函数
的单调区间；
与
的图象有惟一的交点，试求实数
的值.
解析：（Ⅰ）
由
得 
…………………………4分
由
得 
由
得 
故函数
的单调增区间为
，单调减区间为
.
……………………………………8分
（Ⅱ）函数
与
的图象有惟一的交点等价于方程
即
有惟一解
由（Ⅰ）在递减，递增
故在
时取极小值（最小值）
. …………………11分
从而方程有惟一解的充要条件是
.
与的图象有惟一交点时
…………………………1４分 
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
在
处取得极值.
；
，如果
在开区间
上存在极小值，求实数
的取值范围.
=
在
处取得极值.
的值；
的方程
在
上恰有两个不相等的实数根，求实数
的取值范围；
在
处取得极值。
的解析式；
上任意两个自变量的值
，都有
；
可作曲线
的三条切线，求实数
的取值范围。
为实数。
在
处取得极值，求
的值；
对任意
都成立，求实数
的取值范围。
在
处取得极值．
的值；[来源:学+科+网]
的方程
在区间
上恰有两个不同的实数根，求实数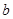
的取值范围．