题目内容
(本小题满分12分〉
设平面直角坐标中,O为原点,N为动点,![]() .过点M作
.过点M作![]() 丄y轴于
丄y轴于![]() ,过N作
,过N作![]() 轴于点N1,
轴于点N1,![]() ,记点T的轨迹为曲线C.
,记点T的轨迹为曲线C.
(I)求曲线C的方程:
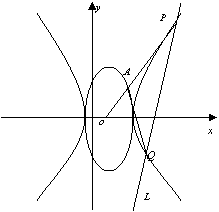
(H)已知直线L与双曲线C:![]() 的右相交于P、Q两点(其中点P在第—象限).线段OP交轨迹C于A,若
的右相交于P、Q两点(其中点P在第—象限).线段OP交轨迹C于A,若![]() ,求直线L的方程.
,求直线L的方程.
【解】(Ⅰ)设T(x,y),点N(x1,y1),则N1(x1,0).又![]() ,
,
即![]()
![]() =(
=(![]() x1,
x1,![]() y1),∴M1(0,
y1),∴M1(0,![]() y1),
y1),![]() =(
=(![]() x1,0),
x1,0),
![]() =(0,y1). …………………3分
=(0,y1). …………………3分
 于是
于是![]() =
=![]() +
+![]() =(
=(![]() x1,y1),………4分
x1,y1),………4分
即(x,y)=(![]() x1,y1).
x1,y1).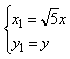 代入|
代入|![]() |=6,得5x2+y2=36.
|=6,得5x2+y2=36.
所求曲线C的轨迹方程为5x2+y2=36.…………………………6分
(Ⅱ)设![]() 由
由![]() 及
及![]() 在第一象限得
在第一象限得![]()
∵![]() ∴
∴![]() 解得
解得![]()
即![]() ………8分,设
………8分,设![]() 则
则![]() ……. ①
……. ①
由![]() 得,
得,![]() ,
,
![]() ,即
,即![]() ……. ② ……………10分
……. ② ……………10分
联立①,②,解得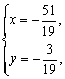 或
或![]() 因点
因点![]() 在双曲线C1的右支,故点
在双曲线C1的右支,故点![]() 的坐标为
的坐标为![]() …11分
…11分
由![]()
![]() 得直线
得直线![]() 的方程为
的方程为![]() 即
即![]() ………12分
………12分

练习册系列答案
相关题目