题目内容
设在三角形ABC中,角A,B,C所对的边分别是a,b,c且满足2a+2c=(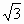 +1)·b
+1)·b
(Ⅰ)求证:2 =(
=(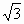 +1)
+1)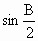 ;
;
(Ⅱ)(文)若A+C=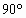 ,试求角C的值.
,试求角C的值.
(理)若A=2C,试求角B的值.
答案:
解析:
解析:
|
解:(Ⅰ)由2a+2c=( 2·2 ∵ 即2 (Ⅱ)(文)若A+C= (*)式可以化为2 即sinC+cosC= 推得sin2C= (Ⅱ)(理)依条件A=2C得B= (*)式可以化为2 ∵ 故sinC= ∵sinC≠0 ∴2cosC-1= 则:cosC= ∴C= |

练习册系列答案
相关题目
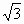 +1)b得2(sinA+sinC)=(
+1)b得2(sinA+sinC)=(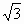 +1)sinB
+1)sinB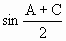 ·
·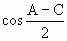 =(
=(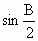
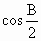 )
)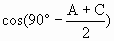 =
=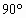 则
则 =
=
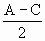 =
=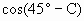 =(
=(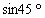
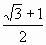
 且
且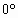 <2C<
<2C<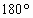 故C=
故C=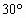 或
或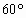
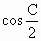 =(
=(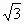 +1)
+1)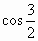 C
C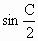 ≠0,2
≠0,2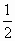 (
(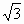 +1)·sinC(2cosC-1)
+1)·sinC(2cosC-1)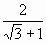 =
=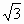 -1
-1 且
且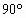
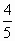 ,
,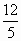 ),并且直线y=0与直线y=x平分三角形ABC的内角.求直线BC的方程.
),并且直线y=0与直线y=x平分三角形ABC的内角.求直线BC的方程.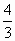 .
.